(能力提升)已知数列 满足
满足 ,(
,( )其中
)其中 ,求数列的通项公式
,求数列的通项公式
已知函数 ,
,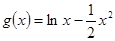 。
。
(1)求函数 的解析式;
的解析式;
(2)若对于任意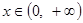 ,都有
,都有 成立,求实数
成立,求实数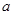 的取值范围;
的取值范围;
(3)设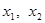 ,
, ,且
,且 ,求证:
,求证: 。
。
如图,已知点D(0,-2),过点D作抛物线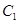 :
: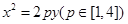 的切线l,切点A在第二象限。
的切线l,切点A在第二象限。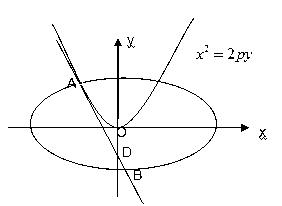
(1)求切点A的纵坐标;
(2)若离心率为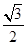 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k, ,①试用斜率k表示
,①试用斜率k表示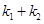 ②当
②当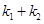 取得最大值时求此时椭圆的方程。
取得最大值时求此时椭圆的方程。
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量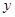 (升)与行驶速度
(升)与行驶速度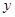 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: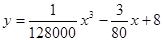 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。
(1)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的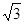 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为
(1)求椭圆 的标准方程;
的标准方程;
(2)若直线 交椭圆
交椭圆 于
于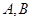 两点,当
两点,当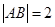 时求直线
时求直线 的方程
的方程
已知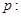 直线
直线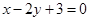 与抛物线
与抛物线 没有交点;
没有交点;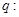 方程
方程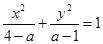 表示椭圆;若
表示椭圆;若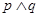 为真命题,试求实数
为真命题,试求实数 的取值范围.
的取值范围.