如图所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角．若在B点悬挂一个定滑轮(不计重力)，某人用它匀速地提起重物．已知重物的质量m="30" kg，人的质量M＝50 kg，g取10 m/s2。试求：
(1)此时地面对人的支持力的大小；
(2)轻杆BC和绳AB所受力的大小．
如图所示,在坐标系Oxy的第一象限中存在沿y轴正方向的匀强电场,场强大小为E.在其他象限中存在匀强磁场,磁场方向垂直于纸面向里.A是y轴上的一点,它到坐标原点O的距离为h;C是x轴上的一点,到O的距离为l.一质量为m、电荷量为q的带负电的粒子以某一初速度沿x轴方向从A点进入电场区域,继而通过C点进入磁场区域,并再次通过A点,此时速度方向与y轴正方向成锐角.不计重力作用.
试求：
（1）粒子经过C点时速度的大小和方向.
（2）磁感应强度的大小B.
1932年，劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如图所示，置于高真空中的D形金属盒半径为R，两盒间的狭缝距离为d，。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的粒子，质量为m、电荷量为+q ，在加速器中被加速，加速电压为U。加速过程中不考虑相对论效应和重力作用。
（1）求粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比；
（2）求粒子从静止开始加速到出口处(电场和磁场)所需的总时间t；
如图所示，电源电动势
内阻
，电阻
。间距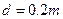
的两平行金属板水平放置，板间分布有垂直于纸面向里、磁感应强度
的匀强磁场。闭合开关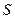
，板间电场视为匀强电场，将一带正电的小球以初速度
沿两板间中线水平射入板间。设滑动变阻器接入电路的阻值为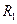
，忽略空气对小球的作用，取
。
（1）当
时，电阻
消耗的电功率是多大？
（2）若小球进入板间做匀速度圆周运动并与板相碰，碰时速度与初速度的夹角为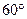
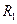，则是多少？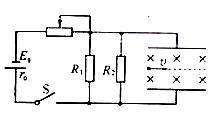
质量为m、长度为L的导体棒MN静止于水平导轨上,通过MN的电流为I,匀强磁场的磁感应强度为B,方向与导轨平面成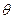
角斜向下,如图所示,求棒MN所受的支持力大小和摩擦力大小.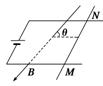
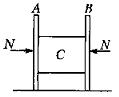
如图，两块固定的竖直平行板A、B间夹着一块长方体木块C，C重6 N，A、B对C的压力大小都是N="10" N。现对C施一外力F，将C从两板间水平匀速拉出，求F的大小和方向。（已知C与A、B间的动摩擦因数均为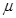
=0.4）