如图所示,飞行器P绕某星球做匀速圆周运动,星球相对飞行器的张角为θ,下列说法正确的是( )
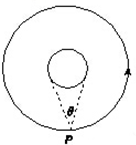
| A.若测得周期和轨道半径,可得到星球的平均密度 |
| B.若测得周期和张角,可得到星球的平均密度 |
| C.轨道半径越大,角速度越大 |
| D.轨道半径越大,速度越大 |
用30N的水平外力F,拉一个静止放在光滑水平面上的的质量为20kg的物体,力作用3s消失,则5s末的速度和加速度分别是()
| A.v = 4.5m/s a=1.5m/s2 | B.v = 7.5m/s a=1.5m/s2 |
| C.v = 4.5m/s a="0" | D.v = 7.5m/s a="0" |
如图3所示,在倾角为α的斜面上,一质量为m的小球被固定的竖直木板挡住,不计一切摩擦,小球对竖直木板的压力的大小为()
| A.mgcosα | B.mgtanα | C. |
D.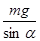 |
作用在物体上同一点的两个大小不变的力,当其夹角由00逐渐增大到1800的过程中,合力的大小将()
| A.先增大后减小 | B.先减小后增大 | C.逐渐增大 | D.逐渐减小 |
下列关于摩擦力的说法中正确的是()
| A.摩擦力的方向总是与物体的运动方向相反 |
| B.静摩擦力的方向总是与物体的相对运动趋势的方向相反 |
| C.摩擦力不一定总是阻碍物体运动,也可以是动力 |
| D.正压力越大,静摩擦力就越大 |
甲乙两个质点同时同地点向同一方向做直线运动,它们的v—t图象如图2所示,则()
| A.甲比乙运动得快 |
| B.甲的平均速度大于乙的平均速度 |
| C.在4s末,乙追上甲 |
| D.乙追上甲时距出发点40m |