(本小题满分12分)如图, 为圆
为圆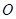 的直径,点
的直径,点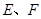 在圆
在圆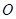 上,
上, ,矩形
,矩形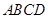 所在的平面和圆
所在的平面和圆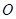 所在的平面互相垂直,且
所在的平面互相垂直,且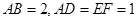 .
.
(1)求证: ;
;
(2)设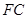 的中点为
的中点为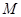 ,求证:
,求证: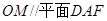 ;
;
(3)设平面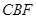 将几何体
将几何体 分成的两个椎体的体积分别为
分成的两个椎体的体积分别为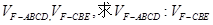 .
.
已知函数f(x)=Asin(ωx+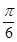 )(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为
)(其中x∈R,A>0,ω>0)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为M(
,且图象上一个最低点为M(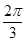 ,-2).
,-2).
(1)求f(x)的解析式;
(2)若x∈[0,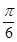 ]求函数f(x)的值域;
]求函数f(x)的值域;
(3)求函数y=f(x)的图象左移 个单位后得到的函数解析式.
个单位后得到的函数解析式.
如图2.3.1-3,MN是异面直线a、b的公垂线,平面α平行于a和b,求证:MN⊥平面α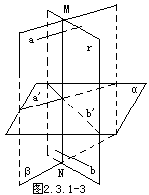
如图,设三角形ABC的三个顶点在平面 的同侧,A
的同侧,A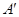 ⊥
⊥ 于
于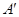 ,B
,B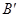 ⊥
⊥ 于
于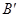 ,C
,C ⊥
⊥ 于
于 ,G、
,G、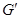 分别是△ABC和△
分别是△ABC和△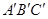 的重心,求证:G
的重心,求证:G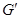 ⊥
⊥
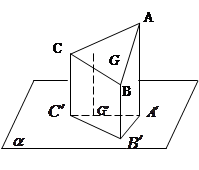
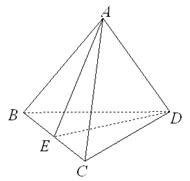
已知:空间四边形 ,
, ,
,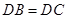 ,求证:
,求证:
求证:经过平面外一点有且只有一个平面和已知平面平行
已知: ∉α
∉α
求证:过点 有且只有一个平面β∥α
有且只有一个平面β∥α