设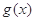 为
为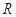 上不恒等于0的奇函数,
上不恒等于0的奇函数,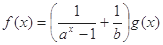 (
(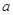 >0且
>0且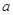 ≠1)为偶函数,则常数
≠1)为偶函数,则常数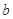 的值为( )
的值为( )
| A.2 | B.1 | C.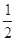 |
D.与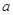 有关的值 有关的值 |
已知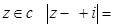 则
则 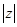 的最小值是 ()
的最小值是 ()
A.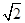 |
B.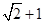 |
C.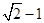 |
D.1 |
如图,第n个图形是由正n+2边形“扩展”而来,(n=1、2、3、…)
则在第n个图形中共有()个顶点。
| A.(n+1)(n+2) | B.(n+2)(n+3) | C. |
D.n |
若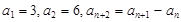 ,则
,则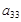 =()
=()
| A.-3 | B.3 | C.-6 | D.6 |
用反证法证明:“若a,b两数之积为0,则a,b至少有一个为0”,应假设()
| A.a,b没有一个为0 | B.a,b只有一个为0 |
| C.a,b至多有一个为0 | D.a,b两个都为0 |
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的R2如下,其中按拟合效果最好的模型是( )
| A.模型1的R2为0.25 | B.模型2的R2为0.80 |
| C.模型3的R2为0.50 | D.模型4的R2为0.98 |