用三段论推理命题:“任何实数的平方大于0,因为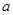 是实数,所以
是实数,所以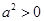 ,你认为这个推理()
,你认为这个推理()
| A.是正确的 | B.大前题错误 | C.小前题错误 | D.推理形式错误 |
复数
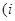 是虚数单位
是虚数单位 的实部是 ()
的实部是 ()
A. |
B. |
C.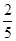 |
D.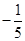 |
设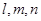 为三条不同的直线,
为三条不同的直线,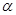 为一个平面,下列命题中正确的个数是()
为一个平面,下列命题中正确的个数是()
①若 ,则
,则 与
与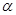 相交
相交
②若 则
则
③若 ||
||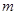 ,
,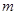 ||
||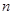 ,
, ,则
,则
④若 ||
||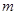 ,
,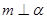 ,
, ,则
,则 ||
||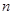
| A.1 | B.2 | C.3 | D.4 |
在如图所示的边长为2的正方形中随机掷一粒豆子,豆子落在正方形内切圆的上半圆(图中阴影部分)中的概率是( )
A.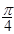 |
B. |
C. |
D. |
从一箱产品中随机地抽取一件,设事件A={抽到一等品},事件B ={抽到二等品},事件C ={抽到三等品},且已知 P(A)=" 0.65" ,P(B)="0.2" ,P(C)=0.1。则事件“抽到的不是一等品”的概率为()
A. 0.7 B. 0.65C. 0.35 D. 0.3