已知球 的半径是1,
的半径是1,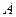 、
、 、
、 三点都在球面上,
三点都在球面上,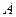 、
、 两点和
两点和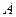 、
、 两点的球面距离都是
两点的球面距离都是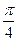 ,
, 、
、 两点的球面距离是
两点的球面距离是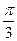 ,则二面角
,则二面角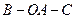 的大小是
的大小是
A.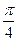 |
B.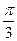 |
C. |
D.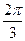 |
已知二面角 的大小为
的大小为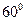 ,
,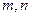 为异面直线,且
为异面直线,且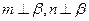 ,则
,则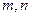 所成的角为
所成的角为
A.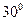 |
B.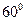 |
C.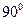 |
D.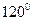 |
若空间中有两条直线,则“这两条直线为异面直线”是“这两条直线没有公共点”的()
| A.充分非必要条件; | B.必要非充分条件; | C.充要条件; | D.非充分非必要条件 |
若空间中有四个点,则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”的()
| A.充分非必要条件; | B.必要非充分条件; | C.充要条件; | D.非充分非必要条件 |
正方体的内切球与其外接球的体积之比为
A.1∶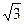 |
B.1∶3 | C.1∶3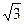 |
D.1∶9 |