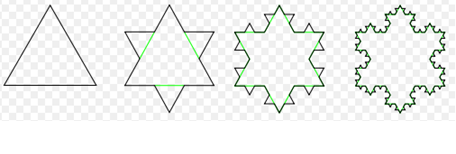
如图是瑞典人科赫（Koch）在1906年构造的能够描述雪花形状的科赫雪花图案．图形的作法是，从一个正三角形开始，把每条边分成三等份，然后以各边的中间长度为底边．分别向外作正三角形，再把“底边”线段抹掉．反复进行这一过程，就会得到一个“雪花”样子的曲线．这是一个极有特色的图形：在图形不断变换的过程中，它的周长趋于无穷大，而其面积却趋于定值．如果假定原正三角形边长为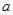
，则可算出下图每步变换后科赫雪花的周长：
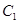=3，
= ，
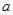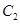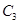= ，…，则
= ．
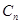若a﹣2b=3，则2a﹣4b﹣5= ．
计算：
．
二次函数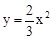
的图象如图，点A0位于坐标原点，点A1，A2，A3…An在y轴的正半轴上，点B1，B2，B3…Bn在二次函数位于第一象限的图象上，点C1，C2，C3…Cn在二次函数位于第二象限的图象上，四边形A0B1A1C1，四边形A1B2A2C2，四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形，∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An﹣1BnAn=60°，菱形An﹣1BnAnCn的周长为 ．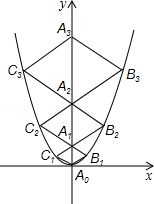
在△ABC中，AB=AC，AB的垂直平分线DE与AC所在的直线相交于点E，垂足为D，连接BE．已知AE=5，tan∠AED=
，则BE+CE= ．
在四张背面完全相同的卡片正面分别画有正三角形，正六边形、平行四边形和圆，将这四张卡片背面朝上放在桌面上．现从中随机抽取一张，抽出的图形是中心对称图形的概率是 ．