古希腊著名的毕达哥拉斯学派把1，3，6，10 …这样的数称为“三角形数”，而把1，4，9，16 …这样的数称为“正方数”． 从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中，符合这一规律的是（ ）
| A．20=6+14 | B．25=9+16 | C．36=16+20 | D．49=21+28 |
如图，以O为顶点且小于180º的角有（）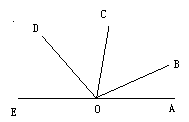
| A．7个 | B．8个 | C．9个 | D．10个 |
如图，下列说法错误的是（）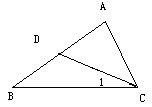
| A．∠B也可以表示为∠ABC |
| B．∠BAC也可以表示为∠A |
| C．∠1也可以表示为∠C |
| D．以C为顶点且小于180º的角有3个 |
如图，M是线段的EF中点，N是线段FM上一点，如果EF="2a," NF=b,则下面结论中错误是( )
| A．MN=a－b | B．MN= a |
| C．EM=a | D．EN=2a－b |
O、P、Q是平面上的三点，PQ=20㎝，OP+OQ=30㎝，那么下列正确的是( )
| A．O在直线PQ外 | B．O点在直线PQ上 |
| C．O点不能在直线PQ上 | D．O点不能在直线PQ上 |
如图，O是线段AC中点，B是AC上任意一点，M、N分别是AB、BC的中点，下列四个等式中，不成立的是( )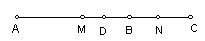
A、MN="OC" B、MO=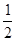
(AC－BC)
C、ON=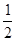(AC-BC) D、MN=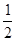(AC-BC)