如图所示，一质量m＝1 kg的木板静止在光滑水平地面上．开始时，木板右端与墙相距L＝0.08 m，一质量m＝1 kg的小物块以初速度v0＝2 m/s滑上木板左端．木板的长度可保证物块在运动过程中不与墙接触．物块与木板之间的动摩擦因数μ＝0.1，木板与墙碰撞后以与碰撞前瞬时等大的速度反弹．取g＝10 m/s2，求：
(1)从物块滑上木板到两者达到共同速度时，木板与墙碰撞的次数及所用的时间．
(2)达到共同速度时木板右端与墙之间的距离．
如图，一质量为m=10kg的物体，由1/4粗糙的圆弧轨道上端从静止开始下滑，到达底端时的速度v=2m/s，然后沿水平面向右滑动1m距离后停止。已知轨道半径R=0.4m，g=10m/s2则：
（1）物体沿轨道下滑过程中克服摩擦力做多少功？
（2）物体滑至圆弧底端时对轨道的压力是多大？
（3）物体与水平面间的动摩擦因数μ是多少？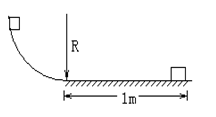
2007年10月24日，我国“嫦娥一号”探月卫星成功发射．“嫦娥一号”卫星开始绕地球做椭圆轨道运动，经过变轨、制动后，成为一颗绕月球做圆轨道运动的卫星．设卫星距月球表面的高度为h，做匀速圆周运动的周期为T．已知月球半径为R，引力常量为G．求：（1）月球的质量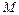
（2）月球表面的重力加速度
如图一辆质量为500kg的汽车通过一座半径为50m的圆弧形拱桥顶部时．g=10m/s2
（1）如果汽车以10m/s的速度经过拱桥的顶部，则汽车对圆弧形拱桥的压力是多大？
（2）如果汽车对圆弧形拱桥的压力恰好为零，则汽车通过拱桥的顶部时速度多大？（计算结果可用根号表示）
(12分)如图所示，质量为M的长方形木板静止在光滑水平面上，木板的左侧固
定一劲度
系数为k的轻质弹簧，木板的右侧用一根伸直的并且不可伸长的轻绳水平地连接在竖直墙上。
绳所能承受的最大拉力为T，一质量为m的小滑块以一定的速度在木板上无摩擦地向左运动，而后压缩弹簧。弹簧被压缩后所获得的弹性势能可用公式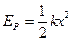
计算，k为劲度系数，x
为弹簧的形变量。
（1）若在小滑块压缩弹簧过程中轻绳始终未断，并且弹簧的形变量最大时，弹簧对木板的弹力大小恰好为T，求此情况下小滑块压缩弹簧前的速度v0；
（2）若小滑块压缩弹簧前的速度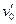
为已知量，并且大于（1）中所求的速度值
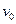，求此情况下弹簧压缩量最大时，小滑块的速度；
（3）若小滑块压缩弹簧前的速度大于（1）中所求的速度值v0，求小滑块最后离开木板时，相对地面速度为零的条件。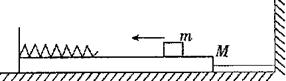
如图所示，在粗糙的水平桌面的边角处有一轻质光滑的定滑轮K，一条不可伸长的轻绳绕过K分别与物块A、B相连，A、B
的质量分别为mA、mB ，开始时系统处于静止状态。现用一水平恒力F拉物块A，使物块B上升。已知当B上升距离为h时，B的速度为v ，重力加速度为g。求：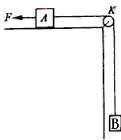
（1）此过程中拉力F
所做的功。
（2）此过程中物块A克服摩擦力所做的功。