在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业.其用氧量包含3个方面:①下潜时,平均速度为 (米/单位时间),单位时间内用氧量为
(米/单位时间),单位时间内用氧量为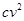 (
(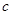 为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为
为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为 (米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为
(米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为 .
.
(1)将 表示为
表示为 的函数;
的函数;
(2)设0< ≤5,试确定下潜速度
≤5,试确定下潜速度 ,使总的用氧量最少.
,使总的用氧量最少.
某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
已知圆 及直线
及直线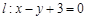 . 当直线
. 当直线 被圆
被圆 截得的弦长为
截得的弦长为 时,
时,
求:(1) 的值;
的值;
(2)过点 并与圆
并与圆 相切的切线方程.
相切的切线方程.
在正方体AC¢中,E、F、G、P、Q、R分别是所在棱AB、BC、BB¢、A¢D¢、D¢C¢、DD¢的中点,求证:平面PQR∥平面EFG。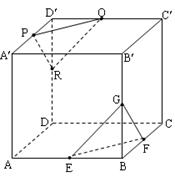
已知指数函数 ,当
,当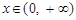 时,有
时,有 ,解关于x的不等式
,解关于x的不等式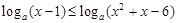
已知函数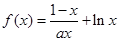 .
.
(Ⅰ)若函数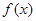 在
在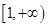 上是增函数,求正实数
上是增函数,求正实数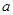 的取值范围;
的取值范围;
(Ⅱ)若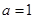 ,
,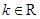 且
且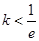 ,设
,设 ,求函数
,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.