古希腊著名的毕达哥拉斯学派把1，3，6，10，…这样的数称为“三角形数”（如图①），而把1，4，9，16，…这样的数称为“正方形数”（如图②）.如果规定a1=1，a2=3，a3=6，a4=10，…；b1=1，b2=4，b3=9，b4=16，…；y1=2a1+b1，y2=2a2+b2，y3=2a3+b3，y4=2a4+b4，…，那么，按此规定，
。
如图，在平面直角坐标系中，点A、B、C的坐标分别是（﹣1，﹣1）、（0，2）、（2，0），点P在y轴上，且坐标为（0，﹣2）．点P关于点A的对称点为P1，点P1关于点B的对称点为P2，点P2关于点C的对称点为P3，点P3关于点A的对称点为P4，点P4关于点B的对称点为P5，点P5关于点C的对称点为P6，点P6关于点A的对称点为P7…，按此规律进行下去，则点P2013的坐标、是 ．
若矩形ABCD的对角线长为10，点E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长是 ．
把直线y=2x﹣1向上平移2个单位，所得直线的解析式是 ．
从﹣3、1、﹣2这三个数中任取两个不同的数，积为正数的概率是 ．
已知a、b为两个连续整数，且a＜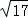
＜b，则a+b= ．