如图,甲、乙两栋高楼的水平距离BD为90米,从甲楼顶部C点测得乙楼顶部A点的仰角α为30°,测得乙楼底部B点的俯角β为60°,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)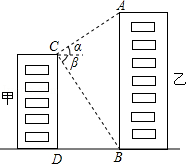
在“走基层,树新风”活动中,青年记者石剑深入边远山区,随机走访农户,调查农村儿童生活教育现状。根据收集的数据字编制了不完整的统计图表如下:
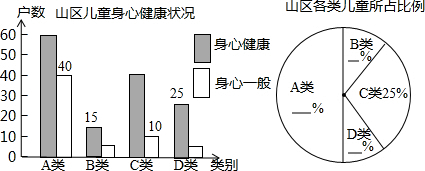
请你用学过的统计知识,解决问题:
(1)记者石剑走访了边远山区多少家农户?
(2)将统计图表中的空缺数据正确填写完整;
(3)分析数据后,请你提一条合理建议.
在一个口袋中有4个完全相同的小球,把它们分别标号l、2、3、4.小明先随机地摸出一个小球,小强再随机地摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y。小明和小强在此基础上共同协商一个游戏规则:当x>y 时小明获胜,否则小强获胜.
(1)若小明摸出的球不放回,求小明获胜的概率.
(2)若小明摸出的球放回后小强再随机摸球,问他们制定的游戏规则公平吗?请说明理由.
端午节吃粽子是中华民族的传统习俗,一超市为了吸引消费者,增加销售量,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母都相同时,消费者就可以获得一次八折优惠价购买粽子的机会.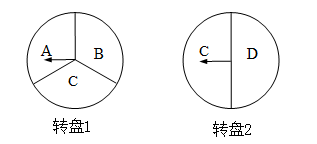
(1)用树状图或列表的方法(只选其中一种)表示出游戏可能出现的所有结果;
(2)若一名消费者只能参加一次游戏,则他能获得八折优惠价购买粽子的概率是多少?
小明和妹妹都想去看科幻电影,要求爸爸去买门票,但爸爸只买回一张门票,那么谁去就成了问题,小明想到一个办法:他拿出一个装有质地、大小相同的 个红球与
个红球与 个白球的袋子,让爸爸摸出一个球,如果摸出的是红球,妹妹去看电影,如果摸出的是白球,小明去看电影。
个白球的袋子,让爸爸摸出一个球,如果摸出的是红球,妹妹去看电影,如果摸出的是白球,小明去看电影。
(1)爸爸说这个办法不公平,请你用概率的知识解释原因。
(2)若爸爸从袋中取出 个白球,再用小明提出的办法来确定谁去看电影,请问摸球的结果是对小明有利还是对妹妹有利,说明理由。
个白球,再用小明提出的办法来确定谁去看电影,请问摸球的结果是对小明有利还是对妹妹有利,说明理由。
某生态示范园要对1号、2号、3号、4号四个新品种共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广.通过实验得知:3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图(部分信息未给出).
(1)实验所用的2号果树幼苗的数量是_______株;
(2)求出3号果树幼苗的成活数,并把图2的统计图补充完整;
(3)你认为应选哪一种果树幼苗进行推广?请通过计算说明理由.