如图所示,一个质量为m,带电量为q的正离子,从D点以某一初速度v0垂直进入匀强磁场。磁场方向垂直纸面向内,磁感应强度为B。离子的初速度方向在纸面内,与直线AB的夹角为60°。结果粒子正好穿过AB的垂线上离A点距离为L的小孔C,垂直AC的方向进入AC右边的匀强电场中。电场的方向与AC平行。离子最后打在AB直线上的B点。B到A的距离为2L。不计离子重力,离子运动轨迹始终在纸面内,求:
(1)粒子从D点入射的速度v0的大小;
(2)匀强电场的电场强度E的大小。
某兴趣小组对一辆自制遥控小车的性能进行研究。他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v—t图象,如图所示(除2s—10s时间段图象为曲线外,其余时间段图象均为直线)。已知在小车运动的过程中,2s—14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行,小车的质量为1.0kg,可认为在整个运动过程中小车所受到的阻力大小不变。求:
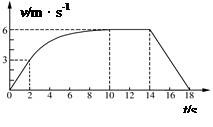
(1)小车所受到的阻力大小;
(2)小车匀速行驶阶段的功率;
(3)小车在加速运动过程中位移的大小。
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里.一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出.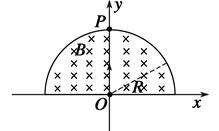
(1)求电场强度的大小和方向.
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经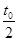 时间恰好从半圆形区域的边界射出.求粒子运动加速度的大小.
时间恰好从半圆形区域的边界射出.求粒子运动加速度的大小.
(3)若仅撤去电场,带电粒子仍从O点射入,但速度为原来的4倍,求粒子在磁场中运动的时间.
如图所示,一带正电的质子以速度v0从O点垂直射入,两个板间存在垂直纸面向里的匀强磁场.已知两板之间距离为d,板长为d,O点是板的正中间,为使粒子能从两板间射出,试求磁感应强度B应满足的条件(已知质子的带电荷量为e,质量为m) 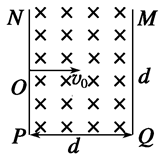
如图所示,两平行金属导轨间的距离L=0.40 m,金属导轨所在平面与水平面夹角θ=37°,在导轨所在的平面内,分布着磁感应强度B=0.50 T、方向垂直于导轨所在平面的匀强磁场.金属导轨的一端接有电动势E=4.5 V、内阻r=0.50 Ω的直流电源.现把一个质量m=0.040 kg的导体棒ab放在金属导轨上,导体棒恰好静止.导体棒与金属导轨垂直且接触良好,导体棒与金属导轨接触的两点间的电阻R0=2.5 Ω,金属导轨电阻不计,g取10 m/s2.已知sin 37°=0.60,cos 37°=0.80,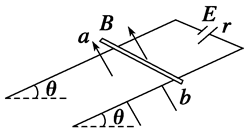
求:(1)通过导体棒的电流;
(2)导体棒受到的安培力大小;
(3)导体棒受到的摩擦力.
如图所示,质量为M=400g的铁板固定在一根轻弹簧上方,铁板的上表面保持水平。弹簧的下端固定在水平面上,系统处于静止状态。在铁板中心的正上方有一个质量为m=100g的木块,从离铁板上表面高h=80cm处自由下落。木块撞到铁板上以后不再离开,两者一起开始做简谐运动。木块撞到铁板上以后,共同下降了l1=2.0cm时刻,它们的共同速度第一次达到最大值。又继续下降了l2=8.0cm后,它们的共同速度第一次减小为零。空气阻力忽略不计,重力加速度取g=10m/s2。求:
⑴ 若弹簧的弹力跟弹簧的形变量成正比,比例系数叫做弹簧的劲度,用k表示.求本题中弹簧的劲度k;
⑵ 从木块和铁板共同开始向下运动到它们的共同速度第一次减小到零的过程中,弹簧的弹性势能增加了多少?
⑶在振动过程中,铁板对木块的弹力的最小值N是多少?