滑板运动是极限运动的鼻祖，许多极限运动项目均由滑板项目延伸而来。如图所示是滑板运动的轨道，BC和DE是两段光滑圆弧形轨道，BC段的圆心为O点，圆心角为60º，半径OC与水平轨道CD垂直，水平轨道CD段粗糙且长8m。一运动员从轨道上的A点以3m/s的速度水平滑出，在B点刚好沿轨道的切线方向滑入圆弧轨道BC，经CD轨道后冲上DE轨道，到达E点时速度减为零，然后返回。已知运动员和滑板的总质量为60kg，B、E两点与水平面CD的竖直高度分别为h和H，且h=2m，H=2.8m，
取10m/s2。求：
（1）运动员从A运动到达B点时的速度大小vB；
（2）轨道CD段的动摩擦因数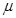
；
（3）通过计算说明，第一次返回时，运动员能否回到B点？如能，请求出回到B点时速度的大小；如不能，则最终静止在何处？
如图（甲）所示，倾角为
的光滑固定斜杆底端固定一个带负电、电量为
的小球A，将一可视为质点的带电小球B从斜杆的底端a点（与A靠得很近，但未接触）静止释放，小球沿斜面向上滑动过程中速度v随位移s的变化图象如图（乙）所示．已知重力加速度g=10m/s2，静电力常量
．求：
（1）小球B的荷质比
；（2）小球B在b点时速度到达最大，求a、b两点的电势差
．
光滑水平轨道上有三个木块A、B、C，质量分别为mA=4m，mB=mC=m，开始时B、C均静止，A以初速度v0向右运动，A与B相撞后分开，B又与C发生碰撞并粘在一起，此后A与B间的距离保持不变。求B与C碰撞前B的速度大小。
如图所示，真空中有一下表面镀反射膜的平行玻璃砖，其折射率n＝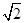
，一束单色光与界面成θ=450角斜射到玻璃砖表面上，最后在玻璃砖的右侧面竖直光屏上出现两个光点A和B，A和B相距h＝4.0cm。已知光在真空中的传播速度c=3.0xl08m/s.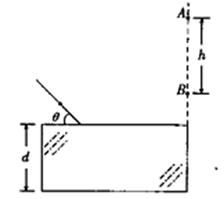
i.画出光路图；
ii.求玻璃砖的厚度
如图所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体。活塞的质量为m，横截面积为S，与容器底部相距h。现通过电热丝缓慢加热气体，当气体的温度为T1时活塞上升了h。已知大气压强为p0。重力加速度为g，不计活塞与气缸间摩擦。
i．求温度为T1时气休的压强；
ii．现停止对气体加热，同时在活塞上缓慢添加砂粒，当添加砂粒的质量为m0时，活塞恰好回到原来位置，求此时气体的温度
如图所示，光滑曲面AB与水平面BC平滑连接于B点，BC右端连接内壁光滑、半径为r的
圆周的细圆管CD，管口D端正下方直立一根劲度系数为k的轻弹簧，轻弹簧一端固定，另一端恰好与管口D端齐平。质量为m的小球在曲面上距BC的高度为3r处从静止开始下滑，小球与BC间的动摩擦因数
，进入管口C端时与圆管恰好无作用力，通过CD后压缩弹簧（弹簧形变量为x时的弹性势能表达式为
）求：
（l）小球达到B点时的速度大小vB；
（2）水平面BC的长度s；
（3）在压缩弹簧过程中小球的最大速度vm。