在青少年科技创新大赛中，某同学展示了其设计的程序控制电动赛车，如图所示．赛车质量M=2.0kg，长L=2m，高h=0.8m，额定功率P=30W．在赛车的最左端放一质量m=1.0kg的物体B（大小可忽略），距赛车右端s=2.0m的地方固定另一个长方体物体C，它的高度为赛车的
，宽度为赛车长的
．已知赛车与物体B间的动摩擦因数μ1=0.4，与地面间的动摩擦因数μ2=0.2，通电后赛车与物体B一起由静止向C运动，与C发生碰撞后电动赛车立即停止．取g=10m/s2，求：
（1）若通电后赛车以额定功率行驶，电动机的工作时间至少为多少，才能使物体B越过C落到地面上？
（2）若通电后开始的一段时间内电动机提供的牵引力F=15N，使赛车做匀加速运动，则电动机的工作时间至少为多少，才能使物体B越过C落到地面上？
从离地高500 m的高空自由下落一个小球，取g="10" m/s2，求：
（1）经过多少时间落到地面；
（2）从开始下落时刻起，在第1 s内的位移，最后1 s内的位移；
（3）落下一半时间的位移.
如图所示，一辆沿平直路面行驶的汽车，速度为54 km/h，刹车后获得加速度的大小是5m/s2，求：
（1）刹车后5s末的速度；
（2）从开始刹车至停止，汽车滑行的距离。
某同学在研究小车运动情况的实验中，获得一条点迹清晰的纸带，已知打点计时器每隔0.02 s打一个计时点，该同学选择A.B.C.D.E、F六个计数点，对计数点进行测量的结果如图所示，单位是cm。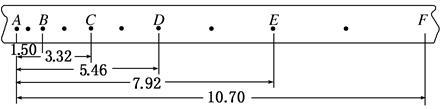
（1）试计算在打下A.F各点时小车的瞬时速度vA.vF各多大？
（2）求小车的加速度大小？
如图所示，平行板电容器竖直放置，两板间距离d=0.10m，左板带正电，右板带负电，电势差U=1.0×103V。一个质量为m=0.2g、带电荷量为q=+1.0×10-7C的小球用长L=0.01m的绝缘细线悬挂于电容器内部的O点，将小球拉到细线呈水平伸直状态的位置A，然后无初速度释放，求：
（1）小球运动至O点正下方B点时，小球的速度大小和绳子拉力的大小（结果可用根号表示）
（2）假如小球运动到B处时，线突然断开，以后发现小球恰能通过B点正下方的C处，求B、C两点间的距离和小球运动至C点时的速度大小（结果可用根号表示）
如图所示，粗糙的绝缘水平面被竖直线PQ分为左、右两部分，左侧有范围足够大、方向水平向右的匀强电场，场强E=20N/C，有一个质量m=2kg、电量q=0.1C的正电滑块（可看作质点）静止在PQ线右侧某一位置。现给滑块一个向左的初速度v0，并从此时刻开始计时，滑块前2s的运动图像如图所示，且2s末时滑块恰好运动到PQ线处。假设最大静摩擦力等于滑动摩擦力，取g=10m/s2，求：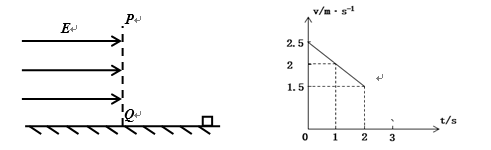
（1）滑块初始位置到PQ线的距离s1
（2）滑块与水平面间的动摩擦因数
（3）滑块能到达左侧最远处到PQ线处的距离s2
（4）滑块最终停在何处