(本小题满分14分)已知抛物线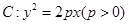 的焦点为
的焦点为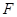 ,准线
,准线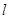 与
与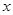 轴的交点为
轴的交点为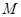 .点
.点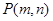 (
( )在抛物线
)在抛物线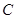 上,且
上,且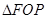 的外接圆圆心到准线
的外接圆圆心到准线 的距离为
的距离为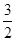 .
.
(Ⅰ)求抛物线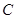 的方程;
的方程;
(Ⅱ)若直线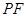 与抛物线
与抛物线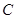 交于另一点
交于另一点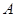 ,证明:
,证明: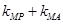 为定值;
为定值;
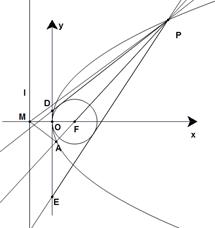
(Ⅲ)过点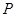 作圆
作圆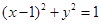 的两条切线,与
的两条切线,与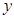 轴分别交于
轴分别交于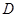 、
、 两点,求
两点,求 面积取得最小值时对应的
面积取得最小值时对应的 值.
值.
在 中,角
中,角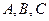 所对的边分别为
所对的边分别为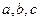 ,且满足
,且满足 ,
, 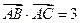 .(I)求
.(I)求 的面积;(II)若
的面积;(II)若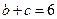 ,求
,求 的值.
的值.
一批救灾物资随26辆汽车从某市以x km/h的速度匀速开往400km处的灾区,为安全起见,每两辆汽车的前后间距不得小于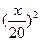 km,问这批物资全部到达灾区,最少要多少小时?
km,问这批物资全部到达灾区,最少要多少小时?
设x,y满足约束条件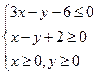 ,若目标函数z=ax+by(a>0,b>0)的值是最大值为12,求
,若目标函数z=ax+by(a>0,b>0)的值是最大值为12,求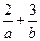 的最小值。
的最小值。
等差数列{an}不是常数列,a5=10,且a5,a7,a10是某一等比数列{bn}的第1,3,5项.(1)求数列{an}的第20项。(2)求数列{bn}的通项公式.
△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.