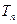(本小题满分14分)经过点 且与直线
且与直线 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为 .点
.点 、
、 在轨迹
在轨迹 上,且关于
上,且关于 轴对称,过线段
轴对称,过线段 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线 ,使直线
,使直线 与轨迹
与轨迹 在点
在点 处的切线平行,设直线
处的切线平行,设直线 与轨迹
与轨迹 交于点
交于点 ,
, .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)证明: ;
;
(Ⅲ)若点 到直线
到直线 的距离等于
的距离等于 ,且△
,且△ 的面积为20,求直线
的面积为20,求直线 的方程.
的方程.
(本小题满分12分)
已知函数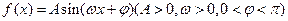 的一个周期的图象,如图(1)求
的一个周期的图象,如图(1)求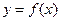 的解析式(2)若函数
的解析式(2)若函数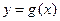 与
与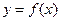 的图象关于直线
的图象关于直线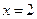 对称,求
对称,求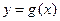 的解析式.
的解析式.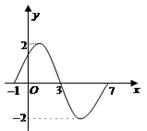
(本小题满分12分)
已知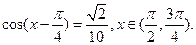
(1)求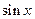 的值;
的值;
(2)求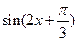 的值.
的值.
设椭圆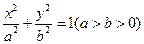 的左,右焦点为
的左,右焦点为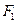 ,
,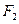 ,(1,
,(1,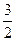 )为椭圆上一点,椭圆的
)为椭圆上一点,椭圆的
长半轴长等于焦距,曲线C是以坐标原点为顶点,以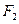 为焦点的抛物线,自
为焦点的抛物线,自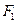 引直线交曲线C于P,Q两个不同的交点,点P关于
引直线交曲线C于P,Q两个不同的交点,点P关于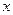 轴的对称点记为M,设
轴的对称点记为M,设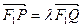 .
.
(1)求椭圆方程和抛物线方程;
(2)证明: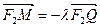 ;
;
(3)若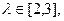 求|PQ|的取值范围
求|PQ|的取值范围
(12分)已知一四棱锥 的三视图,E是侧棱PC上的动点.
的三视图,E是侧棱PC上的动点.
(1)求四棱锥 的体积;
的体积;
(2)若E点分PC为PE:EC=2:1,求点P到平面BDE的距离;
(3)若E点为PC的中点,求二面角D-AE-B的大小.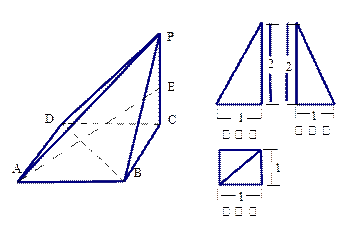
(12分)等比数列{ }的前n项和为
}的前n项和为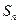 , 已知对任意的
, 已知对任意的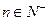 ,点
,点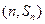 ,
,
均在函数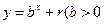 且
且 均为常数)的图像上.
均为常数)的图像上.

( 1)求r的值;
1)求r的值;
(2 )当b=2时,记
)当b=2时,记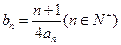 求数列
求数列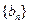 的前
的前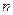 项和
项和