(本题满分14分)已知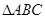 中,
中,  ,
,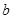 ,
,  分别为角
分别为角  ,
,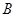 ,
,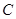 所对的边,
所对的边, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若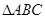 的面积为
的面积为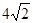 ,
,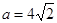 ,求
,求 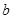 、
、 的长.
的长.
(本题满分14分 )在锐角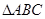 中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2
中,已知内角A、B、C所对的边分别为a、b、c,且满足2sinB(2cos2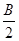 -1)=-
-1)=-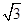 cos2B.
cos2B.
(1)求B的大小;
(2)如果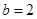 ,求
,求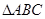 的面积
的面积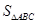 的最大值.
的最大值.
设数列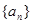 的前
的前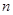 项和为
项和为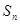 , 且
, 且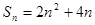 . 设数列
. 设数列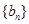 的前
的前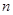 项和为
项和为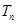 ,且
,且 .(1)求
.(1)求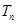 .
.
(2) 设函数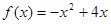 ,对(1)中的数列
,对(1)中的数列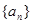 ,是否存在实数
,是否存在实数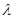 ,使得当
,使得当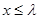 时,
时,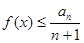 对任意
对任意 恒成立
恒成立
(本题满分15分) 已知函数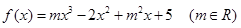 且
且 在
在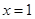 处取得极小值.
处取得极小值.
(1)求m的值。
(2)若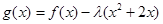 在
在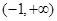 上是增函数,求实数
上是增函数,求实数 的取值范围。
的取值范围。
(本题满分14分)已知在数列 中,
中,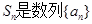 的前n项和,
的前n项和,
(1)求数列 的通项公式;
的通项公式;
(2)令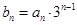 ,数列
,数列 的前n项和为
的前n项和为 求
求
(本题满分14分)在锐角三角形ABC中,已知角A、B、C所对的边分别为a、b、c,且 ,
,
(1)若c2=a2+b2—ab,求角A、B、C的大小;
(2)已知向量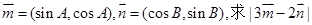 的取值范围。
的取值范围。