设
，
，
表示三条直线，
，
，
表示三个平面，给出下列四个命题：
①若⊥，⊥，则∥；
②若
，是在内的射影，⊥，则⊥；
③若，∥，则∥；
④若⊥，⊥，则∥．其中真命题为（ ）
| A．①② | B．①②③ | C．①②③④ | D．③④ |
下面几种推理是合情推理的是
（1）由圆的性质类比出球的有关性质；
（2）由直角三角形、等腰三角形、等边三角形内角和是
，归纳出所有三角形的内角和都是；
（3）某次考试张军成绩是100分，由此推出全班同学成绩都是100分；
（4）三角形内角和是，四边形内角和是
，五边形内角和是
，由此得凸多边形内角和是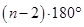
| A．（1）（2） | B．（1）（3） | C．（1）（2）（4） | D．（2）（4） |
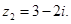则
是
的
| A．充分不必要条件 | B．充要条件 | C．必要不充分条件 | D．不充分不必要条件 |
甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性作试验，并用回归分析方法分别求得相关系数r与残差平方和m如下表；则哪位同学的试验结果体现A、B两变量更强的线性相关性
A．丁B．丙 C．乙 D．甲
| 甲 |
乙 |
丙 |
丁 |
|
| r |
0.82 |
0.78 |
0.69 |
0.85 |
| m |
115 |
106 |
124 |
103 |
若大前提是：任何实数的平方都大于0，小前提是：
，结论是：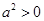
，那么这个演绎推理出错在
| A．大前提 | B．小前提 | C．推理过程 | D．没有出错 |
复数
的共轭复数是
A． |
B． |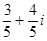
C． |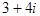
D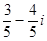． |