如图所示，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动，星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线，A和B分别在O的两侧。引力常数为G。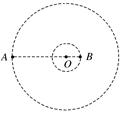
（1）求两星球做圆周运动的周期；
（2）在地月系统中，若忽略其他星球的影响，可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行的周期记为T1。但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期记为T2。已知地球和月球的质量分别为5.98×1024 kg和7.35 ×1022 kg。求T2与T1两者平方之比。（结果保留三位小数）
如图所示，两平行金属板AB中间有互相垂直的匀强电场和匀强磁场。A板带正电荷，B板带等量负电荷，板间电场强度为E；磁场方向垂直纸面向里，磁感应强度为B1。平行金属板右侧有一挡板M，中间有小孔O′，OO′是平行于两金属板的中心线。挡板右侧有垂直纸面向外的匀强磁场，磁场应强度为B2。CD为磁场B2边界上的一绝缘板，它与M板的夹角θ=45°，O′C=a，现有大量质量均为m，含有不同电荷量、不同速度的正、负带电粒子（不计重力），自O点沿OO′方向进入电磁场区域，其中有些粒子沿直线OO′方向运动，并进入匀强磁场B2中，求：
（1）进入匀强磁场B2的带电粒子的速度
（2）能击中绝缘板CD的粒子中，所带电荷量的最大值
（3）绝缘板CD上被带电粒子击中区域的长度
在粗糙的水平面上有两个静止的物体A、B，它们的质量均为
。A与水平面间的动摩擦因数为
，B与水平面间的动摩擦因数
。在水平恒力F="20" N的作用下从静止开始向右做匀加速直线运动，F作用了t="2" s然后撤掉。求：A、B都静止时它们之间的距离L。
如图所示，光滑水平面上一质量为M、长为L的木板右端靠竖直墙壁。质量为m 的小滑块（可视为质点）以水平速度
滑上木板的左端，滑到木板的右端时速度恰好为零。
①求小滑块与木板间的摩擦力大小；
②现小滑块以某一速度
滑上木板的左端，滑到木板的右端时与竖直墙壁发生弹性碰 撞，然后向左运动，刚好能够滑到时木板左端而不从木板上落下，试求
的值。
一半圆形玻璃砖，玻璃的折射率为
，AB为其直径，长度为D, O为圆心，一束宽度恰等于玻璃砖半径的单色平行光束 垂直于AB从空气射入玻璃砖，其中心光线P通过O点，如图所示.M、N为光束边界光线.求：M、N射出玻璃砖后的相交点距O的距离。
如图所示，在平面直角坐标系的第一象限虚线左侧有方向沿y轴负方向的有界匀强电场，电场强度大小为E,第三象限内充满着垂直坐标平面向里的匀强磁场，磁感应强度大小为B。在电场区域内有一动点P,当质量为m电量为q的带正电粒子从P点沿x轴负方向以大小为
的初速度开始运动，粒子能从O点离开电场进入磁场。（不计粒子重力）
(1)求P点的坐标x,y满足的关系；
(2)若当P点位于电场的右边界时，粒子运动到O点的速度大小为2。求第三象限内粒子可能经过的区域的面积。