如图所示，电荷q均匀分布在半球面上，球面的半径为R，CD为通过半球顶点C与球心O的轴线。P、Q为CD轴上在O点两侧，离O点距离相等的二点。如果是带电量为Q的均匀带电球壳，其内部电场强度处处为零，电势都相等。则下列判断正确的是
| A．P点的电势与Q点的电势相等 |
| B．P点的电场强度与Q点的电场强度相等 |
| C．在P点释放静止带正电的微粒（重力不计），微粒将作匀加速直线运动 |
| D．带正电的微粒在O点的电势能为零 |
如图12-3-20所示,闭合导线框的质量可以忽略不计,将它从图示位置匀速拉出匀强磁场.若第一次用0.3 s时间拉出,外力所做的功为W1,通过导线截面的电荷量为q1;第二次用0.9 s时间拉出,外力所做的功为W2,通过导线截面的电荷量为q2,则( )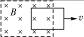
图12-3-20
| A．W1＜W2,q1＜q2 | B．W1＜W2,q1=q2 | C．W1＞W2,q1=q2 | D．W1＞W2,q1＞q2 |
如图12-3-19所示,a、b是同种材料(非超导材料)制成的等长导体棒,静止于水平面内足够长的光滑水平导轨上,b的质量是a的2倍,匀强磁场垂直于纸面向里.若给a4.5 J的初动能使之向左运动,最后a、b速度相同且均为a初速度的
,不计导轨的电阻,则整个过程中a棒产生的热量最大值为( )
图12-3-19
| A．2 J | B．1.5 J | C．3 J | D．4.5 J |
如图12-3-17所示，CDEF是固定的、水平放置的、足够长的“U”形金属导轨，整个导轨处于竖直向上的匀强磁场中，在导轨上架着一个金属棒ab，在极短时间内给ab棒一个水平向右的冲量，使它获得一个速度开始运动，最后又静止在导轨上.则ab棒在运动过程中，就导轨是光滑和粗糙两种情况相比较( )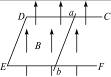
图12-3-17
| A．安培力对ab棒做的功相等 |
| B．电流通过整个回路所做的功相等 |
| C．整个回路产生的总热量不同 |
| D．ab棒动量的改变量相同 |
竖直平面内有一形状为抛物线的光滑曲面轨道,如图12-3-15所示,抛物线方程是y=x2,轨道下半部分处在一个水平向外的匀强磁场中,磁场的上边界是y=a的直线(图中虚线所示),一个小金属环从抛物线上y=b(b＞a)处以速度v沿抛物线下滑,假设抛物线足够长,金属环沿抛物线下滑后产生的焦耳热总量是( )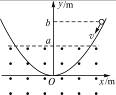
图12-3-15
| A．mgb | B． |
C．mg(b－a) | D． |
粗细均匀的电阻丝围成的正方形线框置于有界匀强磁场中，磁场方向垂直于线框平面，其边界与正方形线框的边平行.现使线框以同样大小的速度沿四个不同方向平移出磁场，如图所示，则在移出过程中线框的一边a、b两点间电势差绝对值最大的是()