(本小题满分12分)
如图,四棱锥P—ABCD中,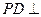 底面ABCD,底面ABCD为正方形,E为PC的中点,点G在BC边上且
底面ABCD,底面ABCD为正方形,E为PC的中点,点G在BC边上且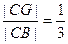 。
。
(Ⅰ)求证: 平面PCD;
平面PCD;
(Ⅱ)点M在AD边上,若PA//平面MEG,
求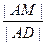 的值。
的值。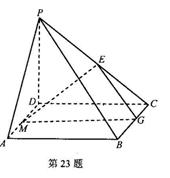
(本小题满分10分)
已知海岛B在海岛A的北偏东45°方向上,A、B相距10海里,小船甲从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船乙从海岛A出发沿北偏15°方向也以2海里/小时的速度移动。
(Ⅰ)经过1小时后,甲、乙两小船相距多少海里?
( Ⅱ)在航行过程中,小船甲是否可能处于小船乙的正东方向?若
Ⅱ)在航行过程中,小船甲是否可能处于小船乙的正东方向?若 可能,请求出所需时间,若不可能,请说明理由。
可能,请求出所需时间,若不可能,请说明理由。

(本小题满分12分) 中,已知
中,已知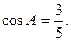
(Ⅰ)求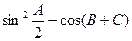 的值;
的值;
(Ⅱ)若 的面积为4,|AB=2,求BC边的长。
的面积为4,|AB=2,求BC边的长。
(本小题满分12分)
函数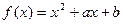 ,不等式
,不等式 的解集为
的解集为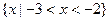
(Ⅰ)求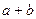 的值;
的值;
(Ⅱ)设函数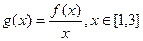 ,求函数
,求函数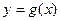 的最小值与对应
的最小值与对应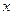 的值。
的值。
(本小题满分10分)
已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示)。
(I)利用所给提示图,作出该几何体的直观图;
(Ⅱ)求该几何体的体积V。