已知函数 R
R ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
.
(1)求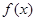 的解析式;
的解析式;
(2)当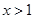 时,
时, 恒成立,求实数
恒成立,求实数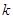 的取值范围;
的取值范围;
(3)设 是正整数,用
是正整数,用 表示前
表示前 个正整数的积,即
个正整数的积,即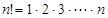 .求证:
.求证: .
.
动点P从边长为1的正方形ABCD的顶点A出发顺次经过B、C、D,再回到A,设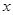 表示P点行程,
表示P点行程,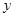 表PA的长,求
表PA的长,求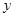 关于
关于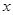 的函数关系式。
的函数关系式。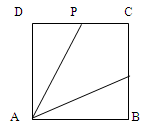
已知函数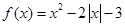 .
.
(Ⅰ)作出函数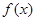 的图像,并根据图像写出函数
的图像,并根据图像写出函数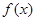 的单调区间;以及在各单调区间上的增减性.
的单调区间;以及在各单调区间上的增减性.
(Ⅱ)求函数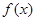 当
当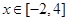 时的最大值与最小值.
时的最大值与最小值.
已知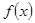 是R上的奇函数,且当
是R上的奇函数,且当 时,
时,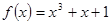 ,求
,求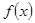 的解析式。
的解析式。
已知集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},
C={x|x2+2x-8=0}.
(Ⅰ)若A=B,求a的值;
(Ⅱ)若A∩B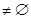 ,A∩C=
,A∩C=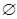 ,求a的值.
,求a的值.
已知集合A= ,B={x|2<x<10},C={x|x<a},全集为实数集R.
,B={x|2<x<10},C={x|x<a},全集为实数集R.
(Ⅰ)求A∪B,(CRA)∩B;
(Ⅱ)如果A∩C≠φ,求a的取值范围.