为声援扬州“运河申遗”，某校举办了一次运河知识竞赛，满分10分，学生得分均为整数，成绩达到6分以上（包括6分）为合格，达到9分以上（包括9分）为优秀．这次竞赛中甲、乙两组学生成绩分布的条形统计图如图所示．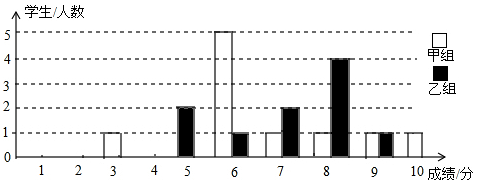
（1）补充完成下面的成绩统计分析表:
| 组别 |
平均分 |
中位数 |
方差 |
合格率 |
优秀率 |
| 甲组 |
6.7 |
|
3.41 |
90% |
20% |
| 乙组 |
|
7.5 |
1.69 |
80% |
10% |
（2）小明同学说:“这次竞赛我得了7分，在我们小组中排名属中游偏上!”观察上表可知，小明是 组的学生；（填“甲”或“乙”）
（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组，请你给出两条支持乙组同学观点的理由．
某市为更好地落实省政府“五水共治”的决策,了解市民最关注的治水问题,调查组随机对部分市民进行电话调查,并将调查结果绘制成如下的两幅不完整的统计图．
根据以上统计图解答问题：
（1）本次被调查的市民有多少？请补全条形统计图；
（2）扇形统计图中“治污水”项目对应的圆心角是_______度；
（3）若该市有居民约400万人,估计其中关心“治污水”项目的有多少人？
如图，为测量一段两岸互相平行的护城河的宽度CD，在河岸边选取A点与B点，测得∠CAB=45°，∠CBA=60°，AB=24米，求这段护城河的宽度CD．（
,结果精确到１m．）
如图,反比例函数
在第一象限的图象经过矩形OABC对角线的交点E，与BC交于点D，若点B的坐标为（6，4）．
（1）求E点的坐标及k的值．
（2）求△OCD的面积．
解方程组：
．
（本小题满分9分）如图1，已知B点坐标是（6
，6），BA⊥x轴于A，BC⊥y轴于C，D在线段OA上，E在y轴的正半轴上,DE⊥BD，M是DE中点，且M在OB上．
（1）点M的坐标是（ ， ），DE= ；
（2）小明在研究动点问题时发现，如果有两点分别在两条互相垂直的直线上做匀速运动，连接这两点所得线段的中点将在同一条直线上运动，利用这一事实解答下列问题，如图2，如果一动点F从点B出发以每秒1个单位长度的速度向点A运动，同时有一点G从点D出发以每秒
个单位长度的速度向点O运动，点H从点E开始沿y轴正方向自由滑动，并始终保持GH=DE,P为FG的中点，Q为GH的中点,F与G两个点分别运动到各自终点时停止运动，分别求出在运动过程中点P、Q运动的路线长．
（3）连接PQ，求当运动多少秒时，PQ最小，最小值是多少？