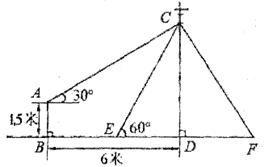
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: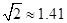 ,
,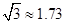 ).
).
已知一次函数y=kx+b的图象经过点(3,-3),且与直线y=4x-3的交点在x轴上.
(1)求这个一次函数的解析式;
(2)此函数的图象经过哪几个象限?
(3)求此函数的图象与坐标轴围成的三角形的面积.
已知一次函数的图象经过点(0,-2),且与两坐标轴围成的三角形面积为3,求一次函数的解析式.
已知一次函数的图象经过A(-2,-3),B(1,3)两点.
(1)求这个一次函数的解析式;
(2)试判断点P(-1,1)是否在这个一次函数的图象上.
已知一次函数的图象经过(-4,15),(6,-5)两点,求一次函数的解析式.
已知一次函数y=kx+b(k≠0)的图象如图所示.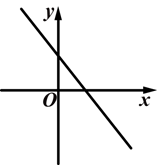
(1)试确定k、b的符号;
(2)若两点(-2,m)、(3,n)在函数图象上,比较m,n的大小