（本题10分）如图，AB为⊙O的直径，EF切⊙O于点D，过点B作BH⊥EF于点H，交⊙O于点C，连接BD.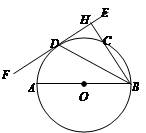
（1）求证：BD平分∠ABH；
（2）如果AB=12，BC=8，求圆心O到BC的距离.
已知
是⊙
的直径，
是⊙的切线，
是切点，
与⊙交于点
.
（1）如图①，若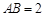
，
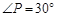，求的长（结果保留根号）；
（2）如图②，若
为的中点，求证：直线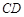
是⊙的切线.
甲、乙、丙、丁四位同学进行一次乒乓球单打比赛，要从中选出两位同学打第一场比赛．
（1）请用树状图法或列表法，求恰好选中甲、丙两位同学的概率；
（2）若已确定甲打第一场，再从其余三位同学中随机选取一位，求恰好选中乙同学的概率．
在如图所示的网格中，每个小方格的边长都是1．
（1）以B为中心，将△ABD顺时针旋转90°，试画出旋转后的图形；
（2）求旋转过程中△ABD扫过图形的面积．
解方程：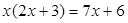
如图，已知函数
的图象与y轴交于点A，一次函数
的图象 经过点B（0，－1），并且与x轴以及的图象分别交于点C、D．
(1)若点D的横坐标为1，求四边形AOCD的面积（即图中阴影部分的面积）；
(2)在第(1)小题的条件下，在y轴上是否存在这样的点P，使得以点P、B、D为顶点的三角形是等腰三角形．如果存在，求出点P坐标；如果不存在，说明理由．
(3)若一次函数的图象与函数的图象的交点D始终在第一象限，则系数k的取值范围是．（请直接写出结果）