小聪和小明沿同一条路同时从学校出发到新华书店查阅资料，学校到新华书店的路程
是4千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达新华书店，图中折线O－A
－B－C和线段OD分别表示两人离学校的路程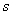
（千米）与所经过的时间
（分钟）之间的函数关系，请根
据图象回答下列问题：
（1）小聪在新华书店查阅资料的时间为________分钟，小聪返回学校的速度为_______千米/分钟．
（2）请你求出小明离开学校的路程s（千米）与所经过的时间t（分钟）之间的函数关系;
（3）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？
吸烟有害健康，为配合“戒烟”运动，某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查，并将调查结果绘制成两幅不完整的统计图：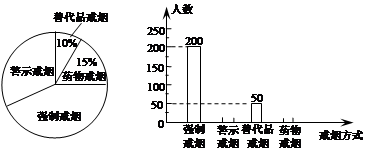
根据统计图解答下列问题：
（1）同学们一共调查了人？
（2）将条形统计图补充完整。
（3）若该社区有1万人，请你估计大约有多少人支持“警示戒烟”这种方式？
（4）为了让更多的市民增强“戒烟”意识，同学们在社区做了两期“警示戒烟”的宣传。在（3）的条件下，若每期宣传后，市民支持“警示戒烟”的平均增长率为20%，则两期宣传后支持“警示戒烟”的市民约有多少人？
在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上．
（1）从A、D、E、F四个点中任意取一点，以所取的这一点及点B、C为顶点画三角形，则所画三角形是等腰三角形的概率是 ；
（2）从A、D、E、F四个点中先后任意取两个不同的点，以所取的这两点及点B、C为顶点画四边形，求所画四边形是平行四边形的概率。（用树状图或列表法求解）．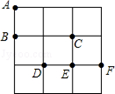
如图，在菱形ABCD中，AC为对角线，点E、F分别是边BC、AD的中点．
（1）求证：△ABE≌△CDF；
（2）若∠B=60°，AB=4，求线段AE的长．
（1）解不等式组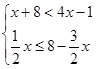 
（2）解方程：
（1）计算： sin60°+|1﹣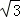
|+
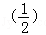﹣1（2）化简：