如图，某边防巡逻队在一个海滨浴场岸边的A点处发现海中的B点处有人求救，便立即派三名救生员前去营救．1号救生员从A点直接跳入海中；2号救生员沿岸边（岸边看成是直线）向前跑50米到C点，再跳入海中；3号救生员沿岸边向前跑200米到离B点最近的D点，再跳入海中．若三名救生员同时从
点出发，他们在岸边跑的速度都是5米/秒，在水中游泳的速度都是2米/秒，∠BAD=45°，请你通过计算说明谁先到达营救地点
．
解不等式组
将两块全等的三角板如图1摆放，其中∠A1CB1＝∠ACB＝90°，∠A1＝∠A＝30°。(1)将图1中△A1B1C绕点C顺时针旋转45°得图2，点
与AB的交点，点Q是
与BC的交点，求证：
=
；(2)在图2中,若AP1=
,则CQ等于多少?(3)将图2中△
绕点C顺时针旋转到△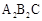
（如图3），点
与AP1的交点．当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
之间存在一个怎样的数量关系?.
已知抛物线的函数关系式：
（其中
是自变量），（1）若点
在此抛物线上，
①求
的值；
②若
，且一次函数
的图象与此抛物线没有交点，请你写出一个符合条件的一次函数关系式（只需写一个，不必写出过程）；（2）设此抛物线与
轴交于点
，
．若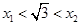
，且抛物线的顶点在直线
的右侧，求的取值范围．
某厂从2007年起开始投入技术改进资金，经技术改进后，某产品的生产成本不断降低，具体数据如下表：
| 年度 |
2007 |
2008 |
2009 |
2010 |
| 投入技改资金x（万元） |
2.5 |
3 |
4 |
4.5 |
| 产品成本y（万元/件） |
7.2 |
6 |
4.5 |
4 |
（1）请你认真分析表中数据，从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律，说明确定是这种函数而不是其他函数的理由，并求出它的解析式；
（2）按照这种变化规律，若2011年已投入技改资金5万元．预计生产成本每件比2010年降低多少万元？
-（3x-5y） +[ 4
，y=-
．