如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．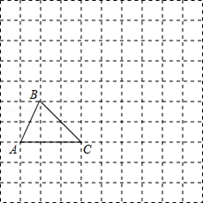
（1）将△ABC绕着点B逆时针旋转90°，得到△A1BC1，请画出△A1BC1；求点A旋转过程中所经过的路径长。
（2）请画一个格点△A2B2C2，使△A2B2C2∽△ABC，且相似比不为1．
（本题10分）．如图，在平面直角坐标系中，一段圆弧经过格点A、B、C，其中点B坐标为（4，3）．
（1）请写出该圆弧所在圆的圆心D的坐标．
（2）⊙D的半径为；
（3）求弧
的长（结果保留π）．
鲁甸地震牵动着全国人民的心，某单位开展了“一方有难，八方支援”赈灾捐款活动．第一天收到捐款10 000元，第三天收到捐款12 100元．
（1）如果第二天、第三天收到捐款的增长率相同，求捐款增长率；
（2）按照（1）中收到捐款的增长速度，第四天该单位能收到多少捐款？
在等腰△ABC中，三边分别为
其中
=5，若关于
的方程
有两个相等的实数根，求△ABC的周长．
已知关于x的方程
．
（1）若此方程有两个不相等的实数根，求a的范围；
（2）在（1）的条件下，当a取满足条件的最小整数，求此时方程的解.
按要求解下列一元二次方程：
（1）
（配方法）；
（2）
（公式法）．