在真空中水平放置平行板电容器,两极板间有一个带电油滴,电容器两板间距为d,当平行板电容器的电压为U0时,油滴保持静止状态,如图所示.当给电容器突然充电使其电压增加ΔU1时,油滴开始向上运动;经时间Δt后,电容器突然放电使其电压减少ΔU2,又经过时间Δt,油滴恰好回到原来位置.假设油滴在运动过程中没有失去电荷,充电和放电的过程均很短暂,这段时间内油滴的位移可忽略不计.重力加速度为g.求: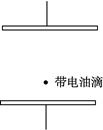
(1)带电油滴所带电荷量与质量之比;
(2)第一个Δt与第二个Δt时间内油滴运动的加速度大小之比;
(3)ΔU1与ΔU2之比.
有两列简谐横波a、b在同一媒质中沿 轴正方向传播,波速均为
轴正方向传播,波速均为 .在t=0时,两列波的波峰正好在
.在t=0时,两列波的波峰正好在 处重合,如图所示.
处重合,如图所示.
①求两列波的周期 和
和 。②求t=0时,两列波的波峰重合处的所有位置。
。②求t=0时,两列波的波峰重合处的所有位置。
一定质量的理想气体从状态A变化到状态B,再变化到状态C,其状态变化过程的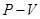 图象如图所示,已知该气体在状态A时的温度为
图象如图所示,已知该气体在状态A时的温度为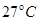 .则:
.则: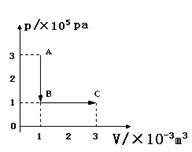
①该气体在状态B、C时的温度分别为多少℃? ②该气体从状态A到状态C的过程中内能的变化量是多大?
如图所示,在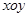 平面内的第一象限内存在沿
平面内的第一象限内存在沿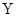 轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度
轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度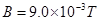 ,有一质量为
,有一质量为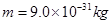 ,电量为
,电量为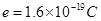 的电子以
的电子以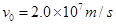 的速度从
的速度从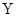 轴的
轴的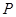 点(0,
点(0,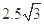 cm)沿
cm)沿 轴正方向射入第一象限,偏转后从
轴正方向射入第一象限,偏转后从 轴的
轴的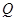 点射入第四象限,方向与
点射入第四象限,方向与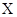 轴成
轴成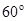 角,在磁场中偏转后又回到
角,在磁场中偏转后又回到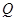 点,方向与
点,方向与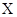 轴也成
轴也成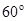 角;不计电子重力.求:
角;不计电子重力.求: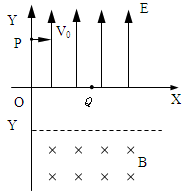
(1)OQ之间的距离及电子通过Q点的速度大小.
(2)若在第四象限内的磁场的边界为直线边界,即在虚线 的下方有磁场,如图中所示,求
的下方有磁场,如图中所示,求 的坐标.
的坐标.
(3)若在第四象限内的磁场为圆形边界的磁场,圆形边界的磁场的圆心坐标的范围.
如图所示,两根足够长的固定平行金属导轨位于同一水平面内,导轨间的距离为 ,导轨上横放着两根导体棒ab和cd.设两根导体棒的质量皆为
,导轨上横放着两根导体棒ab和cd.设两根导体棒的质量皆为 ,电阻皆为
,电阻皆为 ,导轨光滑且电阻不计,在整个导轨平面内都有竖直向上的匀强磁场,磁感强度为
,导轨光滑且电阻不计,在整个导轨平面内都有竖直向上的匀强磁场,磁感强度为 .开始时ab和cd两导体棒有方向相反的水平初速,初速大小分别为
.开始时ab和cd两导体棒有方向相反的水平初速,初速大小分别为 和
和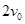 ,求:
,求:
(1)从开始到最终稳定回路中产生的焦耳热.
(2)当ab棒的速度大小变为 ,回路中消耗的电功率的可能值.
,回路中消耗的电功率的可能值.
如图甲所示,在水平地面上放置一个质量为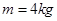 的物体,让其在随位移均匀减小的水平推力作用下运动,推力
的物体,让其在随位移均匀减小的水平推力作用下运动,推力 随位移
随位移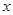 变化的图象如图乙所示。已知物体与地面之间的动摩擦因数为
变化的图象如图乙所示。已知物体与地面之间的动摩擦因数为 ,
,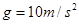 .求:
.求:
(1)运动过程中物体的最大加速度为多少?
(2)距出发点多远时物体的速度达到最大?
(3)物体在水平面上运动的最大位移是多少?