为了迎接太空时代的到来,美国国会通过一项计划:在2050年前建造成太空升降机,就是把长绳的一端搁置在地球的卫星上,另一端系住升降机,放开绳,升降机能到达地球上,科学家可以控制卫星上的电动机把升降机拉到卫星上。已知地球表面的重力加速度g=10m/s2,地球半径R=6400km,地球自转周期为24h。某宇航员在地球表面测得体重为800N,他随升降机垂直地面上升,某时刻升降机加速度为10m/s2,方向竖直向上,这时此人再次测得体重为850N,忽略地球公转的影响,根据以上数据( )
| A.可以求出升降机此时所受万有引力的大小 |
| B.可以求出此时宇航员的动能 |
| C.可以求出升降机此时距地面的高度 |
| D.如果把绳的一端搁置在同步卫星上,可知绳的长度至少有多长 |
一矩形线圈在匀强磁场中绕垂直于磁场方向的轴匀速转动,线圈中产生的电动势为e=Emsinωt。若将线圈的转速加倍,其它条件不变,则产生的电动势为()
| A.Emsin2ωt | B.2Emsinωt | C.2Emsin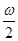 t t |
D.2Emsin2ωt |
图中矩形线圈abcd在匀强磁场中以ad边为轴匀速转动,产生的电动势瞬时值为e = 5sin20tV,则以下判断正确的是()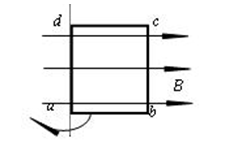
| A.当线圈平面与中性面垂直时,线圈中的感应电流为0 |
| B.当线圈平面与中性面重合时,线圈中的感应电动势为5V |
| C.此交流电的频率为10/πHz |
| D.线圈转动一周,感应电流的方向改变一次 |
如图所示,固定放置在同一水平面内的两根平行长直金属导轨的间距为d,其右端接有阻值为R的电阻,整个装置处在竖直向上的磁感应强度大小为B的匀强磁场中.一质量为m(质量分布均匀)的导体杆ab垂直于导轨放置,且与两导轨保持良好接触,杆与导轨之间的动摩擦因数为μ。当杆在水平向左、垂直于杆的恒力F作用下从静止开始沿导轨运动距离l时,速度恰好达到最大(运动过程中杆始终与导轨保持垂直).设杆接入电路的电阻为r,导轨电阻不计,重力加速度大小为g。则此过程
A.杆的速度最大值为 |
B.流过电阻R的电荷量为 |
| C.恒力F做的功与摩擦力做的功之和等于杆动能的变化量 |
| D.恒力F做的功与安培力做的功之和大于杆动能的变化量 |
如图所示,一端接有定值电阻的平行金属轨道固定在水平面内,通有恒定电流的长直绝缘导线垂直并紧靠轨道固定,导体棒与轨道垂直且接触良好.在向右匀速通过M、N两区的过程中,导体棒所受安培力分别用FM、FN表示.不计轨道电阻,以下叙述正确的是
| A.FM向右 | B.FN向左 | C.FM逐渐减小 | D.FN逐渐减小 |
如图所示,阻值为R的金属棒从图示位置ab分别以v1、v2的速度沿光滑导轨(电阻不计)匀速滑到a′b′位置,若v1∶v2=1∶2,则在这两次过程中
| A.回路电流I1∶I2=1∶2 |
| B.产生的热量Q1∶Q2=1∶2 |
| C.通过任一截面的电荷量q1∶q2=1∶2 |
| D.外力的功率P1∶P2=1∶2 |