如图所示，水平桌面上静止着质量为M的斜面体，斜面与水平方向的夹角为θ，质量为m的物块放置在斜面上，斜面体与水平间的动摩擦因数为μ1，物块与斜面间的动摩擦因数为μ2，已知μ2＞tanθ．现用一从零逐渐增大的水平拉力F拉斜面体直到物块与斜面体发生相对滑动．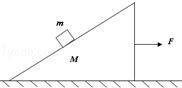
（1）物块相对斜面体滑动时所受摩擦力大小；
（2）从施加F到物块与斜面体发生相对滑动这一过程中，拉力F的最大值；
（3）定性画出斜面体M的速度随时间的变化图象．
如图所示，在光滑绝缘的水平轨道上方同时存在着水平向右的匀强电场和垂直纸面向里的匀强磁场，磁场的磁感应强度B＝0.1T。一质量m=1.0×10-2kg、带电量q＝+1.0×10-2C可视为质点的物块，从轨道上的M点无初速度释放，当该物块沿直线运动到达轨道上的N点时，恰好对轨道无压力，求此时速度多大？（g＝10m/s2）
(14分)如图所示，一群（不计重力）质量为m，电量为q的带正电的粒子从左侧小孔进入电场强度为E，磁感应强度为B的速度选择器（方向如图所示）后，紧接着从右侧小孔进入垂直于纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B，从磁场Ⅰ的边界MN上的a点进入磁场Ⅰ，经过时间
穿过磁场Ⅰ后进入右边磁场Ⅱ并按某一路径再返回到磁场Ⅰ的边界MN上的某一点b（图中末画出），（途中虚线为磁场区域的分界面）求：
（1）带电粒子进入磁场时的速度；
（2）中间场区的宽度d；
（3）粒子从a点到b点所经历的时间tab；
（4）入射点a到出射点b的距离；
(13分)如图所示，虚线上方有场强为E的匀强电场，方向竖直向下，虚线上下有磁感应强度相同的匀强磁场，方向垂直纸面向外，ab是一根长为L的绝缘细杆，沿电场线放置在虚线上方的场中，b端在虚线上.将一套在杆上的带正电的小球从a端由静止释放后，小球先做加速运动，后做匀速运动到达b端。已知小球与绝缘杆间的动摩擦因数μ=0.3，小球重力忽略不计，当小球脱离杆进入虚线下方后，运动轨迹是半圆，圆的半径是L/3，求带电小球从a到b运动过程中克服摩擦力所做的功与电场力所做功的比值。
(11分)如图所示，在倾角为θ的光滑斜面上垂直纸面放置一根长为L、质量为m的直导体棒ab，通以方向向里的电流，电流强度为I，重力加速度为g，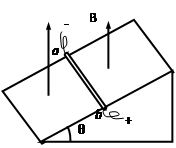
（1）若加竖直向上的匀强磁场，使导体棒静止在斜面上，求所加磁场的磁感应强度B的大小；
（2）若匀强磁场的大小、方向都可以改变，要使导体棒能静止在斜面上，求所加磁场的磁感应强度B的最小值和所对应方向。
(10分) 如图所示，A、B为平行板电容器，两板相距d，接在电压为U的电源上，在A板的中央有一小孔M（两板间电场可视为匀强电场）．今有一质量为m的带电质点，自A板上方与A板相距也为d的O点由静止自由下落，穿过小孔M后到达距B板
的N点时速度恰好为零．求：
(1) 带电质点的电荷量，并指出其带电性质；
(2) 在保持与电源相连的情况下，A板往下移
的距离．质点仍从O点由静止自由下落，求质点下落速度为零时距B板的距离．