已知数列{an}是各项均为正数且公比不等于1的等比数列．对于函数y=f（x），若数列{lnf（an）}为等差数列，则称函数f（x）为“保比差数列函数”．现有定义在（0，+∞）上的如下函数：
①
，
②f（x）=x2，
③f（x）=ex，
④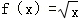
，
则为“保比差数列函数”的所有序号为（ ）
| A．①② | B．③④ | C．①②④ | D．②③④ |
随机抽取某中学甲、乙两面个班10名同学，测量他们的身高（单位：cm）后获得身高数据的茎叶图如图甲所示，在这20人中，记身高在
内的人数依次为
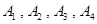，图乙是统计样本中身高在一定范围内的人数的算法流程图，则下列说法正确的是（）
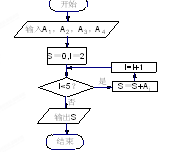
| A．由图甲可知甲、乙两班中身高的中位数较大的是甲班，图乙输出的S的值为18 |
| B．由图甲可知甲、乙两班中身高的中位数较大的是乙班，图乙输出的S的值为18 |
| C．由图甲可知甲、乙两班中身高的中位数较大的是乙班，图乙输出的S的值为16 |
| D．由图甲可知甲、乙两班中身高的中位数较大的是甲班，图乙输出的S的值为16 |
给出下面四个命题：
①分别与两条异面直线都相交的两条直线一定是异面直线；
②分别与两个平行平面都平行的两条直线一定平行；
③垂直于同一个平面的两条直线平行；
④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。
其中为真命题的是（）
| A．①③ | B．①④ | C．③④ | D．②③ |
某校为了研究学生的性别和对待某一活动的态度（支持和不支持两种态度）的关系，运用
列联表进行独立性检验，经计算
，则所得到的统计学结论是：有（）的把握认为“学生性别与支持该活动有关系”。
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
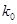2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
A、0.1% B、1% C、99% D、99.9%
正弦函数是奇函数，
是正弦函数，因此是奇函数，以上推理（）
| A．小前提不正确 | B．大前提不正确 | C．结论正确 | D．全不正确 |
复数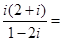
（）
| A．i | B． |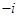
C．1 | D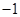． |