对数列{an}，如果∃k∈N*及λ1，λ2，…，λk∈R，使an+k=λ1an+k﹣1+λ2an+k﹣2+…+λkan成立，其中n∈N*，则称{an}为k阶递归数列．给出下列三个结论：
①若{an}是等比数列，则{an}为1阶递归数列；
②若{an}是等差数列，则{an}为2阶递归数列；
③若数列{an}的通项公式为
，则{an}为3阶递归数列．
其中，正确结论的个数是（ ）
| A．0 | B．1 | C．2 | D．3 |
椭圆
(φ为参数)的离心率为（）
A． |
B． |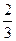
C． |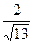
D． |
若直线y=x+t与椭圆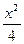
+y2=1相交于A、B两点,当t变化时,|AB|的最大值为( )
A.2 B.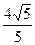
C.
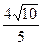D.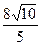
直线y=x+m与椭圆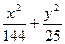
=1有两个公共点,则m的取值范围是( )
| A．(-5,5) | B．(-12,12) | C．(-13,13) | D．(-15,15) |
设直线l:2x+y+2=0关于原点对称的直线为l′,若l′与椭圆x2+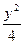
=1的交点为A、B,点P为椭圆上的动点,则使△PAB面积为
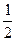的点P的个数为( )
A.1 B.2 C.3 D.4
椭圆
=1的准线平行于y轴,则实数m的取值范围是()
A．0<m< |
B．m<且m≠0 |
| C．m>且m≠1 |
D．m>0且m≠1 |