定义方程f（x）=f′（x）的实数根x0叫做函数f（x）的“新驻点”，若函数g（x）=x，h（x）=ln（x+1），φ（x）=x3﹣1的“新驻点”分别为α，β，γ，则α，β，γ的大小关系为（ ）
| A．γ＞α＞β | B．β＞α＞γ | C．α＞β＞γ | D．β＞γ＞α |
函数y＝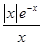
的图像的大致形状是( )
设定义在[－1，7]上的函数y＝f(x)的图像如图所示，则关于函数y＝
的单调区间表述正确的是( )
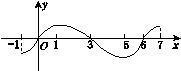
| A．在[－1，1]上单调递减 |
| B．在(0，1]上单调递减，在[1，3)上单调递增 |
| C．在[5，7]上单调递减 |
| D．在[3，5]上单调递增 |
下列函数中，既是偶函数又在区间(0，＋∞)上单调递减的是( )
A．y＝ |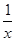
B．y＝e－x | C．y＝－x2＋1 | D．y＝lg |x| |
已知幂函数f(x)的图像经过点(9，3)，则f(2)－f(1)＝( )
| A．3 | B．1－ |
C．－1 |
D．1 |
已知a>0，且a≠1，loga3<1，则实数a的取值范围是( )
| A．(0，1) | B．(0，1)∪(3，＋∞) |
| C．(3，＋∞) | D．(1，2)∪(3，＋∞) |