计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制数的对应关系如下表:
| 十六进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
| 十进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
例如,用十六进制表示:E+D=1B,则B×F (“×”表示通常的乘法运算)等于( )
A.A5 B.BF C.165 D.B9
下面几种推理过程是演绎推理的是
A.某校高二共有10个班,1班有51人,2班有5 3人,3班有52人,由此推测各班都超过50人. 3人,3班有52人,由此推测各班都超过50人. |
B.两条直线平行,同旁内角互补,如果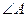 和 和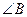 是两条平行直线的同旁内角,则 是两条平行直线的同旁内角,则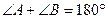 . . |
| C.由平面三角形的性质,推测空间四面体性质. |
D.在数列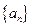 中 中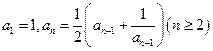 ,由此归纳出 ,由此归纳出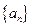 的通项公式. 的通项公式. |
在复平面内,复数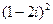 对应的点位于
对应的点位于
| A.第一象限 | B.第二象限 | C.第三象限 |
D.第四象限 |
经济学中的“蛛网理论”(如下图),假定某种商品的“需求—价格”函数的图像为直线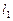 ,“供给—价格”函数的图像为直线
,“供给—价格”函数的图像为直线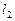 ,它们的斜率分别为
,它们的斜率分别为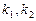 ,
,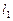 与
与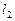 的交点
的交点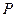 为“供给—需求”平衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点
为“供给—需求”平衡点,在供求两种力量的相互作用下,该商品的价格和产销量,沿平行于坐标轴的“蛛网”路径,箭头所指方向发展变化,最终能否达于均衡点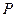 ,与直线
,与直线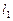 、
、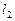 的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点
的斜率满足的条件有关,从下列三个图中可知最终能达于均衡点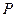 的条件为 ( )
的条件为 ( )
A.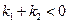 |
B.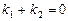 |
C.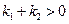 |
D.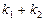 可取任意实数 可取任意实数 |
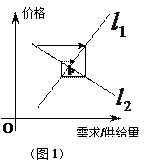 |
|||||
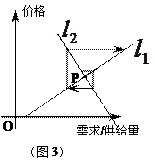 |
|||||
 |
|||||
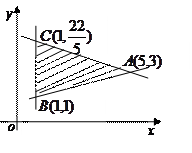
已知平面区域如右图所示,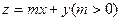 在平面区域内取得最大值的最优解有无数多个,则
在平面区域内取得最大值的最优解有无数多个,则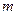 的值为()
的值为()
A.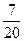 |
B.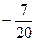 |
C.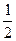 |
D.不存在 |
在坐标平面内,与点A(1,2)的距离为1,且与点B(5,5)的距离为d的直线共有4条,则d的取值范围是()
| A.0<d<4 | B.d≥4 |
| C.4<d<6 | D.以上结果都不对 |