请仔细阅读以下材料:
已知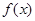 是定义在
是定义在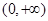 上的单调递增函数.
上的单调递增函数.
求证:命题“设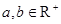 ,若
,若 ,则
,则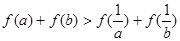 ”是真命题.
”是真命题.
证明 :因为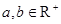 ,由
,由 得
得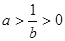 .
.
又因为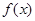 是定义在
是定义在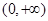 上的单调递增函数,
上的单调递增函数,
于是有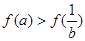 . ①
. ①
同理有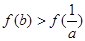 . ②
. ②
由①+ ②得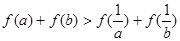 .
.
故,命题“设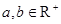 ,若
,若 ,则
,则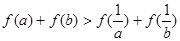 ”是真命题.
”是真命题.
请针对以上阅读材料中的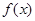 ,解答以下问题:
,解答以下问题:
(1)试用命题的等价性证明:“设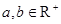 ,若
,若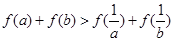 ,则:
,则: ”是真命题;
”是真命题;
(2)解关于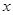 的不等式
的不等式 (其中
(其中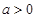 ).
).
(本小题满分14分)
已知函数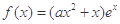 ,其中e是自然数的底数,
,其中e是自然数的底数, .
.
(1)当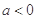 时,解不等式
时,解不等式 ;
;
(2)当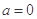 时,求正整数k的值,使方程
时,求正整数k的值,使方程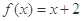 在[k,k+1]上有解;
在[k,k+1]上有解;
(3)若 在[-1,1]上是单调增函数,求
在[-1,1]上是单调增函数,求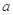 的取值范围.
的取值范围.
(本小题满分13分)
在数列 中,已知
中,已知 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求证:数列 是等差数列;
是等差数列;
(Ⅲ)设数列 满足
满足 ,求
,求 的前n项和
的前n项和 .
.
(本小题满分12分)
如图:在三棱锥D-ABC中,已知 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且

(1)求三棱锥D-ABC的表面积;
(2)求证AC⊥平面DEF;
(3)若M为BD的中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.
(本小题满分12分)
已知  且
且 ;
; :集合
:集合 ,且
,且 .若
.若 ∨
∨ 为真命题,
为真命题, ∧
∧ 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,
,
设向量 ,
, ,
, 
(Ⅰ)若 ∥
∥ ,求证:
,求证: 为等腰三角形;
为等腰三角形;
(Ⅱ)若 ⊥
⊥ ,边长
,边长 ,
, ,求
,求 的面积.
的面积.