阅读下面的文字，解答问题：（本题8分）
大家知道
是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，但是由于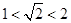
，所以的整数部分为1，将减去其整数部分1，所得的差就是其小数部分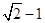
，根据以上的内容，解答下面的问题：
（1）
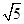的整数部分是________，小数分部是________；
（2）
的整数部分是________，小数小数分部是________；
（3）若设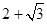
整数部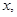分是
小数部分是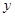
，求
的值．
如图，一转盘被等分成三个扇形，上面分别标有-1，1，2，指针位置固定，转动转盘后任其自由停止后，某个扇形会恰好停在指针所指的位置，得到这个扇形上相应的数．若指针恰好指在等分线上，则需重新转动转盘．
（1）若小静转动转盘一次，则她得到负数的概率为；
（2）小宇和小静分别转动转盘一次，若两人得到的数相同，则称两人“不谋而合”．请用列表法(或画树状图)求出两人“不谋而合”的概率．
如图，在边长为1的小正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别为A（-2，3）、B（-3，1）.△AOB绕点O顺时针旋转90°后得到△A1OB1。
（1）画出△A1OB1；
（2）点A1的坐标为；
（3）点A旋转到点A1所经过的路线长为_____________.（结果保留π）
已知关于
的方程
－（k＋2）＋2k＝0
（1）说明：无论k取何值，方程总有实数根；
（2）若方程有两个相等的实数根，求出方程的根.
先化简，再求值：
，其中a＝
－1，b=.
（1）计算：(－1)2011＋(
－3)0＋
；（2）解方程：
(－4)=5.