如图，已知二次函数
的图像经过A（－1，－1），C（1，3）.
（1）求二次函数的解析式并画出它的图像；
（2）直接写出点A关于抛物线对称轴的对称点A'的坐标；
（3）求该抛物线上到x轴的距离为2的所有点的坐标．
观察图3和图4，分别说出它们由哪些基本图形组成，运用了哪些图形变换？
如图，三个圆是同心圆，最大圆的半径为1，求图中阴影部分的面积．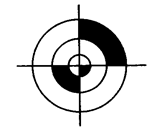
数学兴趣小组的同学想利用树影测树高，在阳光下他们测得一根长为1米的竹竿的影长为0.9米，此刻测量树影，发现树的影子不全落在地上，有一部分影子落在墙壁上，如图所示，同学们测得地面上的影子长为3.6米，墙壁上的影子长为0.9米．又知以树和地面上的树影为边的三角形与同一时刻以竹竿和地面上的影子为边的三角形是一个相似变换，求这棵树的实际高度．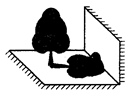
如图，一长方形的长为10，宽为8，将它的长和宽各减少1，得到一个新的小长方形，则原长方形与新长方形是相似图形吗？为什么？
如图，D，E分别是△ABC边AB，AC上的点，DE∥BC：（1）找出图中的相似三角形；（2）写出三组成比例的线段．