已知直线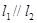 ,直线
,直线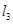 与
与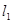 、
、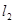 分别交于
分别交于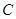 、
、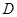 两点,点
两点,点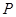 是直线
是直线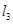 上的一动点
上的一动点
(1)如图①,若动点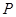 在线段
在线段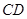 之间运动(不与
之间运动(不与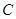 、
、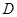 两点重合),问在点
两点重合),问在点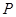 的运动过程中是否始终具有
的运动过程中是否始终具有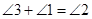 这一相等关系?试说明理由;
这一相等关系?试说明理由;
(2)如图②,当动点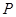 在线段
在线段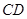 之外且在的上方运动(不与
之外且在的上方运动(不与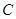 、
、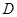 两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;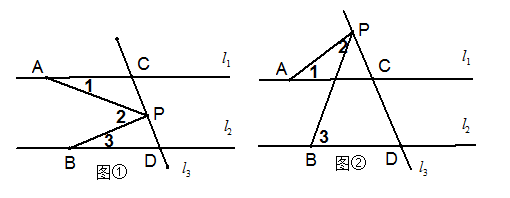
已知:如图,AC=AB,∠1=∠2,∠3=∠4.求证:AE=AD.
如图,已知E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别是C,D.求证:OE垂直平分CD.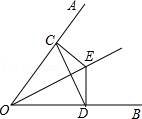
如图所示,在△ABC中: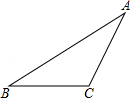
(1)画出BC边上的高AD和中线AE.
(2)若∠B=30°,∠ACB=130°,求∠BAD和∠CAD的度数.
如图所示,点E,F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
如图,用三个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个大长方形.根据图示数据,解答下列问题: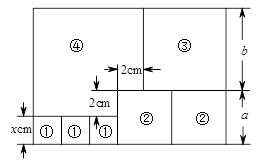
(1)用含x的代数式表示:a= cm,b= cm;
(2)用含x的代数式表示大长方形的周长,并求x=3时大长方形的周长.