所示,MN、PQ为平行光滑导轨,其电阻忽略不计,与地面成30°角固定。N、Q间接一电阻R′=1.0Ω,M、P端与电池组和开关组成回路,电动势E=6V,内阻r=1.0Ω,导轨区域加有与两导轨所在平面垂直的匀强磁场。现将一条质量m=40g,电阻R=1.0Ω的金属导线置于导轨上,并保持导线ab水平,已知导轨间距L=0.1m,当开关S接通后导线ab恰静止不动.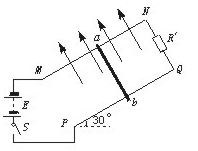
(1)试计算磁感应强度大小;
(2)若ab静止时距地面的高度为0.5m,断开S,ab沿导轨下滑到底端时的速度大小为2.0m/s。试求该过程中R′上得到的电热.(取g=10m/s2)
(10分)在“勇气号”火星探测器着陆的最后阶段,着陆器降落到火星表面上,再经过多次弹跳才停下来.假设着陆器第一次落到火星表面弹起后,到达最高点时高度为h,速度方向是水平的,速度大小为v0,求它第二次落到火星表面时速度的大小,计算时不计火星大气阻力.已知火星的一个卫星的圆轨道的半径为r,周期为T,火星可视为半径为r0的均匀球体.
(10分) 一架喷气式飞机,质量m=5×103kg,起飞过程中从静止开始滑跑的路程为s =5.3×102m时,达到起飞的速度v =60m/s,在此过程中飞机受到的平均阻力是飞机重量的0.02倍(k=0.02),求飞机受到的牵引力.(结果保留两位有效数字)
如图所示,光滑水平面上有A、B、C三个物块,其质量分别为mA = 2.0kg,mB = 1.0kg,mC = 1.0kg.现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做功108J(弹簧仍处于弹性限度内),然后同时释放A、B,弹簧开始逐渐变长,当弹簧刚好恢复原长时,C恰以4m/s的速度迎面与B发生碰撞并粘连在一起.求: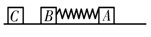
(1)弹簧刚好恢复原长时(B与C碰撞前)A和B物块速度的大小?
(2)当弹簧第二次被压缩时,弹簧具有的最大弹性势能为多少?
如图所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s,试回答下列问题:
(1)写出x=1.0m处质点的振动函数表达式;
(2)求出x=2.5m处质点在0~4.5s内通过的路程及t=4.5s时的位移.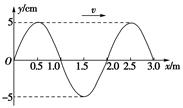
某发电站,通过升压变压器、输电线和降压变压器,把电能输送给生产和照明组成的用户,发电机输出功率为100kW,输出电压是400V,升压变压器原、副线圈的匝数之比为1:25,输电线上功率损失为4%,用户所需电压为220V,求:
(1)输电线的电阻和降压变压器的匝数比为多少?
(2)若有60kW分配给生产,其余电能用来照明,那么可供40W的电灯多少盏?