若圆C经过(1,0),(3,0)两点,且与y轴相切,则圆C的方程为( )
A. |
B.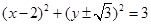 |
C. |
D.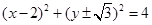 |
以下是面点师一个工作环节的数学模型:如图,在数轴上截取与闭区间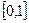 对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标
对应的线段,对折后(坐标1所对应的点与原点重合)再均匀的拉成一个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的坐标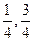 变成
变成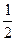 ,原来的坐标
,原来的坐标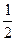 变成1,等等)。则区间
变成1,等等)。则区间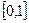 上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与1重合的点所对应的坐标是
上(除两个端点外)的点,在第二次操作完成后,恰好被拉到与1重合的点所对应的坐标是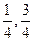 ,那么在第
,那么在第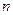 次操作完成后
次操作完成后 ,恰好被拉到与1重合的点对应的坐标是()
,恰好被拉到与1重合的点对应的坐标是()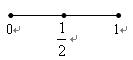
A.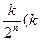 为 为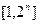 中所有奇数) 中所有奇数) |
B.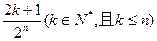 |
C.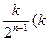 为 为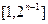 中所有奇数) 中所有奇数) |
D. |
已知函数 ,
, ,构造函数
,构造函数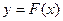 ,定义如下:当
,定义如下:当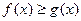 时,
时, ;当
;当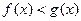 时,
时,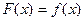 ,那么
,那么
| A.有最大值3,最小值-1 | B.有最大值7 ,无最小值 ,无最小值 |
| C.有最大值3,无最小值 | D.无最大值,也无最小值 |
下列有关样本相关系数的说法不正确的是
A.相关系数用来衡量变量 与 与 之间的线性相关程度 之间的线性相关程度 |
B.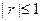 ,且 ,且 越接近于1,相关程度越大 越接近于1,相关程度越大 |
C.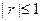 ,且 ,且 越接近于0,相关程度越小 越接近于0,相关程度越小 |
D.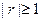 ,且 ,且 越接近于1,相关程度越大 越接近于1,相关程度越大 |
如图,在梯形ABCD中,AB//DC,AB=
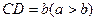 。若
。若 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为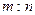 ,则可推算出:
,则可推算出: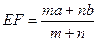 ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设 ,
,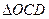 的面积分别为
的面积分别为 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为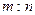 ,则
,则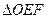 的面积
的面积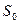 与
与 的关系是( )
的关系是( )
A  B
B 
C D
D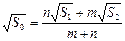
函数 的定义域为一切实数,则实数m的取值范围是
的定义域为一切实数,则实数m的取值范围是
| A.[0,4) | B.(0,4) | C.[4,+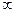 ) ) |
D.[0,4] |