如图,在平面直角坐标系xOy中,抛物线 与x轴交于A(1,0)、
与x轴交于A(1,0)、
B(5,0)两点.
(1). 求抛物线的解析式和顶点C的坐标;
(2). 设抛物线的对称轴与x轴交于点D,将∠DCB绕点C按顺时针方向旋转,角的两边CD和CB与x轴分别交于点P、Q,设旋转角为 (0°<
(0°< <90°)
<90°)
①当 等于多少度时,△CPQ是等腰三角形?
等于多少度时,△CPQ是等腰三角形?
②设 ,求s与t之间的函数关系式.
,求s与t之间的函数关系式.
建设新农村,农村大变样.向阳村建起了天然气供应站,气站根据实际情况,每天从零点开始至凌晨4点,只打开进气阀,在以后的16小时(4∶00-20∶00),同时打开进气阀和供气阀,20∶00-24∶00只打开供气阀,已知气站每小时进气量和供气量是一定的,下图反映了某天储气量 与
与 (小时)之间的关系.
(小时)之间的关系. 
(1). 求0∶00-20∶00之间气站每小时增加的储气量;
(2). 求20∶00-24∶00时, 与
与 的函数关系式,并画出函数图象;
的函数关系式,并画出函数图象;
(3). 照此规律运行,从这天零点起三昼夜内,经过__小时气站储气量达到最大?最大值为___ .(请把答案直接写在在横线上,不必写过程)
.(请把答案直接写在在横线上,不必写过程)
方形ABCD的AB边为直径,在正方形内部作半圆,圆心为O,DF切半圆于点E,交AB的延长线于点F,BF=4.求:
(1). cos∠F的值;
(2). BE的长.
某省为解决农村饮用水问题,省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2008年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2010年该市计划投资“改水工程”1176万元.
(1). 求A市投资“改水工程”的年平均增长率;
(2). 从2008年到2010年,A市三年共投资“改水工程”多少万元?
已知:直线a∥b,点A、B在直线a上,点C、D在直线b上,如图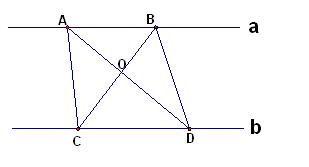
(1). 若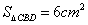 ,则
,则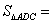
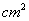
(2). 若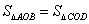 ,那么
,那么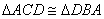 吗?说明你的理由。
吗?说明你的理由。