程序框图如图所示,若输入a的值是虚数单位i,则输出的结果是( )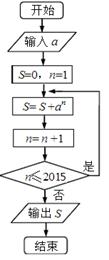
A. |
B. |
C. |
D. |
下列向量中,能作为表示它们所在平面内所有向量的基底的是
| A.e1="(0,0)," e2 =(1,-2) ; | B.e1=(-1,2),e2 ="(5,7);" |
| C.e1=(3,5),e2 =(6,10); | D.e1="(2,-3)" ,e2 =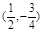 |
以下描述正确的是
| A.第一象限角是锐角 |
| B.小于90度的角是锐角 |
| C.三角形的内角是第一或第二象限角 |
| D.终边相同的角不一定相等 |
在 中, ,设点 满足 .若 ,则 ()
| A. | B. | C. | D. | 2 |
将函数 (其中 )的图像向右平移 个单位长度,所得图像经过点 ,则 的最小值是
| A. | B. | 1 | C. | D. | 2 |
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为()
| A. | |
| B. | 且 |
| C. | |
| D. |