德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数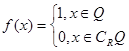
被称为狄利克雷函数，其中R为实数集，Q为有理数集，则关于函数
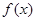有如下四个命题：①
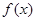；②函数是偶函数；③任取一个不为零的有理数T, 
对任意的
恒成立；④存在三个点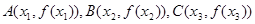
，使得
为等边三角形.其中真命题的个数是
| A．1 | B．2 | C．3 | D．4 |
已知函数f(x)是奇函数，且在(－∞，＋∞)上为增函数，若x，y满足等式f(2x2－4x)＋f(y)＝0，则4x＋y的最大值是( )
| A．10 | B．-6 | C．8 | D．9 |
下列命题中错误的是( )
A矩形的两条对角线相等；
B等腰梯形的两条对角线互相垂直；
C平行四边形的两条对角线互相平分；
D正方形的两条对角线互相垂直且相等．
关于函数y=-5x，下列说法正确的是（ ）
| A．y随x的增大而增大 |
| B．不论x为何值，总有y＞0 |
| C．必经过二、四象限 |
| D．图象必经过点（0，5） |
P1（x1，y1），P2（x2，y2）是正比例函数y=-x图象上的两点，则下列判断正确的是（ ）
| A．y1＞y2 |
| B．y1＜y2 |
| C．当x1＜x2时，y1＞y2 |
| D．当x1＜x2时，y1＜y2 |
已知函数y=kx的函数值随x的增大而增大，则函数的图象经过（ ）
| A．第一、二象限 |
| B．第一、三象限 |
| C．第二、三象限 |
| D．第二、四象限 |