如图所示,长L=1.5 m、高h=0.45 m、质量M=10 kg的长方体木箱在水平面上向右做直线运动.当木箱的速度v0=3.6 m/s时,对木箱施加一个方向水平向左的恒力F=50 N,并同时将一个质量m=1 kg的小球轻放在木箱上距右端处的P点(小球可视为质点,放在P点时相对于地面间的速度为零),经过一段时间,小球脱离木箱落到地面.已知木箱与地面间的动摩擦因数μ=0.2,而小球与木箱之间的摩擦不计.取g=10 m/s2,求: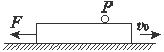
(1)小球从开始离开木箱至落到地面所用的时间;
(2)小球放上P点后,木箱向右运动的最大位移;
(3)小球离开木箱时,木箱的速度.
一客运列车匀速行驶,其车轮在铁轨间的接缝处会产生周期性撞击。坐在该客车中的某旅客测得从第1次到第16次撞击声之间的时间间隔为10.0s。在相邻的平行车道上有一列货车,当该旅客经过货车车尾时,货车恰好从静止开始以恒定加速度沿客车行进方向运动。该旅客在此后的20.0s内,看到恰好有30节货车车厢被他连续超过。已知每根铁轨的长度为25.0m,每节货车车厢的长度为16.0m,货车车厢间距忽略不计。求:
(1)客车运行速度的大小;
(2)货车运行加速度的大小。
)一辆汽车以10m/s的速度沿平直公路匀速运动,司机发现前方有障碍物立即减速,以 0.2m/s2的加速度做匀减速运动,求减速后一分钟内汽车的位移?
(13分)一辆汽车刹车后做匀减速直线运动,初速度为20m/s ,加速度大小为2m/s2。试求该汽车:⑴刹车后第4s末的速度?⑵ 刹车后4s内的平均速度?⑶从刹车到停止汽车发生的位移?
木块A、B分别重50 N和60 N,它们与水平地面之间的动摩擦因数均为0.25;夹在A、B之间的轻弹簧被压缩了2 cm,弹簧的劲度系数为400 N/m.系统置于水平地面上静止不动.现用F=1 N的水平拉力作用在木块B上,如图所示,求力F作用后木块A、B所受摩擦力的大小.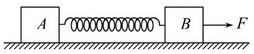
神舟十号于2013年6月11日成功发射,在轨飞行15天,升空后再和目标飞行器天宫一号对接,并首次开展中国航天员太空授课活动。手控交会对接是中国航天事业的历史新高度,是中国航天强国梦的新起点。据预测,2020年前后,中国将走进更强大的太空时代。假设中国宇航员在某行星上从高75m处自由释放一重物,测得在下落最后1s内所通过的距离为27m.求:
(1)重物下落的总时间;
(2)该星球表面的重力加速度.