已知椭圆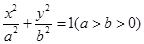 经过点
经过点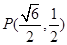 ,离心率为
,离心率为 ,动点M(2,t)(
,动点M(2,t)( ).
).
(1)求椭圆的标准方程;
(2)求以OM为直径且截直线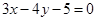 所得的弦长为2的圆的方程;
所得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,证明线段ON的长为定值,并求出这个定值.
(本小题满分12分)如图,已知 是抛物线
是抛物线 上两个不同点,且
上两个不同点,且 ,
,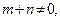 直线
直线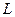 是线段
是线段 的垂直平分线.设椭圆E的方程为
的垂直平分线.设椭圆E的方程为 .
.
(Ⅰ)当 在
在 上移动时,求直线
上移动时,求直线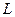 斜率
斜率 的取值范围;
的取值范围;
(Ⅱ)已知直线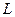 与抛物线
与抛物线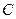 交于A、B两个不同点,
交于A、B两个不同点, 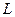 与椭圆
与椭圆 交于P、Q两个不同点,设AB中点为
交于P、Q两个不同点,设AB中点为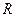 ,
,
PQ中点为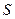 ,若
,若 ,求
,求 离心率的范围.
离心率的范围.
(本题满分12分 )已知等差数列 满足:
满足: ,
, ,该数列的前三项分别加上1,1,3后顺次成为等比数列
,该数列的前三项分别加上1,1,3后顺次成为等比数列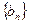 的前三项.
的前三项.
(Ⅰ)分别求数列 ,
,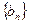 的通项公式
的通项公式 ,
, .
.
(Ⅱ)设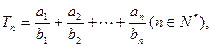 若
若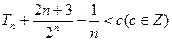 恒成立,求c的最小值.
恒成立,求c的最小值.
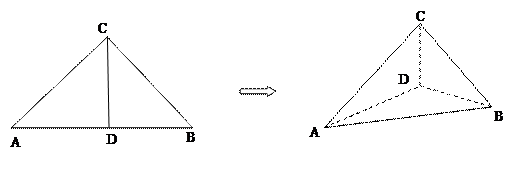
(本题满分12分 )如图,在等腰直角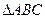 中,
中, ,
,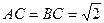 ,
, ,
, 为垂足.沿
为垂足.沿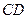 将
将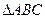 对折,连结
对折,连结 、
、 ,使得
,使得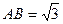 .
.
(1)对折后,在线段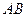 上是否存在点
上是否存在点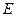 ,使
,使 ?若存在,求出
?若存在,求出 的长;若不存在,说明理由;
的长;若不存在,说明理由;
(2)对折后,求二面角 的平面角的大小.
的平面角的大小.
(本题满分12分 )某班同学利用国庆节进行社会实践,对 岁的人群随机抽取
岁的人群随机抽取 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图: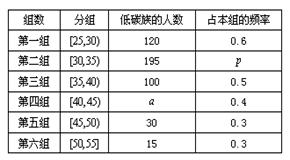

(Ⅰ)补全频率分布直方图并求 、
、 、
、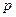 的值;
的值;
(Ⅱ)从 岁年龄段的“低碳族”中采用分层抽样法抽取
岁年龄段的“低碳族”中采用分层抽样法抽取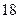 人参加户外低碳体验活动,其中选取
人参加户外低碳体验活动,其中选取 人作为领队,记选取的
人作为领队,记选取的 名领队中年龄在
名领队中年龄在 岁的人数为
岁的人数为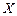 ,求
,求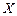 的分布列和期望
的分布列和期望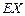 .
.
(本小题满分12分)在 中,
中, 分别为角
分别为角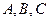 的对边,向量
的对边,向量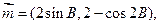
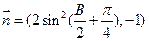 ,且
,且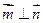 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若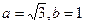 ,求
,求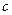 的值.
的值.