力F1作用在物体上产生的加速度a1=3m/s2,力F2作用在该物体上产生的加速度a2=4m/s2,则F1和F2同时作用在该物体上,产生的加速度的大小不可能为 ( )
| A.8m/s2 | B.5m/s2 | C.1m/s2 | D.7m/s2 |
比荷为e/m 的电子以速度v0沿AB边射入边长为口的等边三角形的匀强磁场区域中(如图).为使电子从BC边穿出磁场,磁感应强度B的取值范围为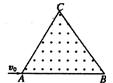
A.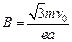 |
B.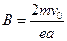 |
C. |
D. |
一列横波的传播方向上有两点P和Q,两点间距离30m,它们的振动图象如图
| A.若P点距波源近,则波速可能为V=60m/s |
| B.若P点距波源近,则波速可能为V=100m/s |
| C.若Q点距波源近,则波速可能为V=300m/s |
| D.若Q点距波源近,则波速可能为V=30m/s |
如图两根不计电阻的光滑金属导轨MN、PQ并排固定在同一绝缘水平面上,将两根完全相同的导体棒a、b静止置于导轨上,两棒与导轨接触良好且与导轨垂直,整个装置处于竖直向下的匀强磁场中。已知两导轨间的距离为L,导体棒的质量均为m,现突然给导体棒b一水平瞬间冲量使之产生一向右的初速度vo,下列说法正确的是
| A.据上述已知量可求出棒a的最终速度 | B.据上述已知量可求出棒a上产生的总焦耳热 |
| C.据上述已知量可求出通过棒a的最大电量 | D.据上述已知量可求出棒a、b间的最大间距 |
如图男同学站立不动,女同学坐在秋千上来回摆动.下列说法正确的是
| A.男同学吹口哨,女同学从高处向低处运动过程中,她感觉哨声音调变低 |
| B.男同学吹口哨,女同学从低处向高处运动过程中,她感觉哨声音调变高 |
| C.女同学经过C点时男同学开始按表记时并从1开始计数,当数到N次时记录的时间为t.因此判断女同学摆动周期T=2t/N |
| D.女同学经过C点时男同学开始按表记时并从1开始计数,当数到N次时记录的时间为t.因此判断女同学摆动周期T=2t/(N-1) |
如图电路中,两个灵敏电流表G1和G2的零点都在刻度盘中央.当电流从G表“+”接线柱流入时,指针向右摆;电流从“-”接线柱流入时,指针向左摆.在电路接通达到稳定状态后再断开的瞬间,下面哪个说法符合实际?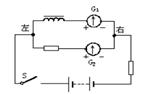
| A.G1指针向右摆,G2指针向左摆 | |
| B.G1指针向左摆,G2指针向右摆 | |
| C.G1、G2的指针都向左摆 | D.G1、G2的指针都向右摆 |