已知:如图,∠1=∠2,DE=DC,EF=AC.求证:EF∥AB.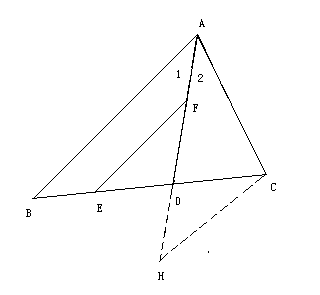
已知关于x的方程 =x+
=x+ 与
与 =3x-2的解互为倒数,求m的值?
=3x-2的解互为倒数,求m的值?
(1)已知x<-4,化简│-x│+│x+4│-│x-4│;
(2)把一批图书分给某班学生阅读,如果每人分3本,则剩余20本,如果每人分4本,则还缺25本。问有多少本图书?多少名学生?
(1)计算:-( )2×9-2×(-
)2×9-2×(- )÷
)÷ +4×(-0.5)2
+4×(-0.5)2
(2)解方程: -
- =
= -1
-1
(1)先化简,再求值2(m2n+mn2)-2(m2n-1)-3(mn2+1),其中m=-2,n=2
(2)将下列各数在数轴上表示出来,并用“<”连接:-22,-(-1),0,-│-2│,-2.5,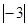
学校门口经常有小贩搞摸奖活动.某小贩在一只黑色的口袋里装有只有颜色不同的50只小球,其中红球1只,黄球2只,绿球10只,其余为白球.搅拌均匀后,每2元摸1个球.奖品的情况标注在球上(如下图)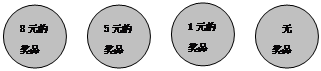
(1)如果花2元摸1个球,那么摸不到奖的概率是多少?
(2)如果花4元同时摸2个球,那么获得10元奖品的概率是多少?